Kurvendiskussion Lösung?
Abend,
es wäre total lieb, wenn jemand die Lösung der Aufgaben reinschreiben könnte, damit ich diese mit meinem Ergebnis vergleiche.
Liebe Grüße

3 Antworten
a) ableiten: f‘(x)= 4x^3 -8x f“(x)=12x^2 -8
b) Die Funktion fällt erst im negativen Bereich dann steigt sie wieder dann fällt sie wieder für positive kleine x Werte und danach steigt sie wieder
c) NST findet man durch Nullsetzen also f(x)=0
x^4 -4x^2=0 Form den Ausdruck um in
x^2 (x^2 - 4)=0 damit die Gleichung erfüllt ist ist entweder der rechte oder linke Teil des Produkts gleich null also
x^2 = 0 => bei x=0 eine Nst
x^2-4 = 0 => bei x=2 und x=-2 Nullstelle
d) dafür die erste Ableitung null setzen
f‘(x)= 4x^3 -8x=0
wieder x ausklammern und eine 4
4x(x^2 -2)=O
4x=0 => x=0 eine extremstelle
x^2 -2=0 => x=+/–wurzel(2) extremstelle
e) die extrempunkte in f“ einsetzen
f“(0) = 12*0^2 -8 = -8 => HP
f“(Wurzel(2))= 12*2-8 = 16 =>TP
f“(–Wurzel(2)) = 12*2-8=16 => TP
Wenn der Wert f“(x)>0 ist es ein Tiefpunkt
wenn der Wert f“<0 ist es ein HP
f) Wendepunkt zweite Ableitung null setzen:
f“(x)=12*x^2 -8=0
12x^2=8 => x^2= 2/3 => x= +/- Wurzel(2/3)
zum überprüfen noch in die dritte Ableitung einsetzen
f“‘(x)= 24x
g) du kennst jetzt alle kritischen Punkte. Zeichne ein Koordinaten System und trage die Punkte der Nullstellen/extremstellen ein und verbinde sie
Danke sehr für deine Antwort und Zeit.
Mein Ergebnis sieht anders aus und ich habe auch keine dritte Ableitung 😂 Schaue gerne in den Kommentar, auf dem ich mein Ergebnis gesendet habe.
Machen wir es doch umgekehrt. Du stellst deine Lösungen (möglichst incl. Rechenweg) mit sauberem Aufschrieb hier ein. Ich kontrolliere dann morgen früh gerne.
Dann fehlt ja nur noch der Graph der Funktion. Dafür kannst du z.B. desmos verwenden.
a) erste Ableitung= 4x^3 — 8x
zweite Ableitung= 12x^2 —8
b) Kommt aus dem zweiten Quartal und geht in den ersten Quartal.
c) Nullstellen (Habe Substitution genutzt)
u1 = 4
u2 = 0
(keine Ahnung ob das richtig ist 🤣)
d) Extrempunkte
E1 (1/-3)
E2 (0/0)
e) Nachweis
—8 Maximum
100 Minimum
f) Wendepunkte ( Habe zwei?)
W1(0.81/—2.19)
W2(-0,81/2,19)
Fertig. Graph mache ich erst wenn es auch richtig ist .
Liebe Grüße
Hmm, ich glaube du benötigst noch ein wenig Lernaufwand beim Verständnis zum Lösen von quadratischen Gleichungen. Ein Beispiel
c) Nullstellen (Habe Substitution genutzt)
u1 = 4
u2 = 0
Zunächst, warum verwendest du Substitution? Es ist doch
x^4 - 4x² = x²(x² - 4) (ein x² ausgeklammert).
Wenn du jetzt die Nullstellen suchst, kannst du ausnutzen dass (dritte binomische Formel!) x² - 4 = (x - 2)(x + 2). Nun verwende den Satz vom Nullprodukt, um die Nullstellen 0, 2 und -2 zu finden. Die Fehler ziehen sich durch alle Bereiche der Lösung hindurch. Bei den Wendepunkten (die du aufgrund deiner anderen Frage richtig berechnet hast wenn du beim zweiten auch noch -2,19 einsetzt) achte bitte darauf die Wurzel in deinem Aufschrieb stehen zu lassen oder wenigstens ... zu verwenden um anzudeuten dass deine Lösung nicht exakt ist. Ansonsten haben andere schon genug dazu geschrieben.
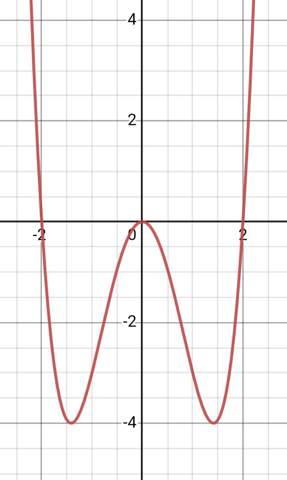
So sieht die Kurve aus.
🤓
a) hast du richtig.
b) Hier sollst du bestimmt die Achsensymmetrie angeben und dass die Werte für x--> ±∞ gegen +∞ gehen.
Hallo,
ich habe bei den E Punkten —3,99 ist das trotzdem richtig wenn ich es so aufschreibe und darf ich da mit ruhigem Gewissen 4 schreiben ? —4 natürlich
4 bzw. -4 ist richtig. Du hast mit gerundeten Zahlen gerechnet, daher die Abweichung.
Also muss ich doch liebe aufrunden oder habe ich einen Fehler gemacht
Es ist besser mit √2 zu rechnen als mit 1,4142. Dann gibt dein Taschenrechner auch das richtige Ergebnis an.
Gut ich habe aber die Zahl nicht nicht in die Wurzel eingegeben, sondern in f(x)
Ich verstehe diese Rechnung nicht sorry das ich nerve aber wieso die Wurzel ? Und wenn ich statt 1,41 2 in die f(x) einsetze bekomme ich 0 statt 4
x=√2≈1,4142
Wenn du f(2) ausrechnest, bist du bei den Nullstellen. Das siehst du auch in der Abbildung in meiner Antwort. Die Tiefpunkte sind aber nicht bei x=2, sondern bei x=±√2.
Ja das habe ich aber diese Tiefpunkte eingesetzt in f(x) macht 3,99 bzw 4 für den Y Punkt des Extrempunktes.
Ich glaube jetzt haben wir uns verstanden 🥺
Gerne bin aber nur bis Wendepunkt angelangt. Wenn ich mehr habe schicke ich es.