Konvergenz Divergenz von Reihen?
Hallo, kann mir jemand bei den beiden Aufgaben helfen oder hat jemand einen guten Ansatz?
(an)n sei die Folge der Fibonacci-Zahlen (a0=1, a1=1 und an+2 := an+1 +an)
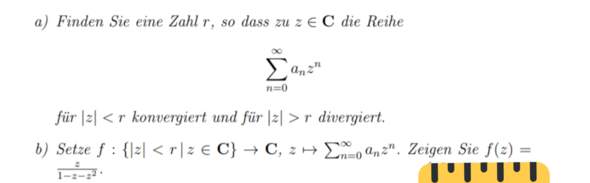
1 Antwort
Bei a) ist der sogenannte Konvergenzradius der Potenzreihe gefragt. Den kann man hier beispielsweise mit dem Quotientenkriterium bestimmen, genauer gesagt mit...
Weiterer Hinweis: Man kann zeigen, dass
ist. Dabei bezeichnet Φ = (1 + √(5))/2 den sogenannten Goldenen Schnitt.
============
Zu b): Multipliziere f(z) mit (1 - z - z²) und zeige, dass sich das dann zu z vereinfachen lässt.
======Ergänzung======
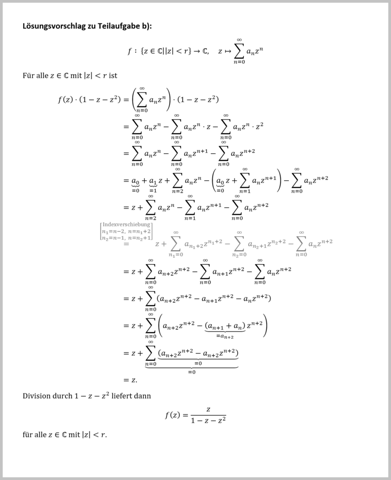
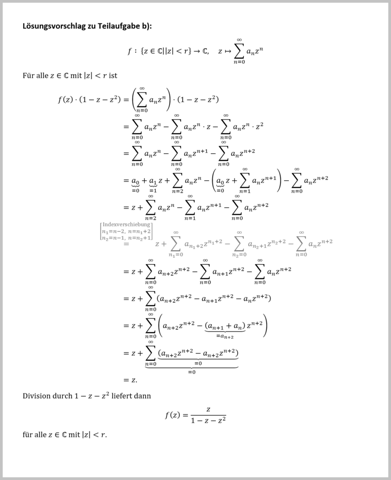
Lösungsvorschlag zu Teilaufgabe b):
Sorry, aber private Anfragen nehme ich hier auf gutefrage.net nicht an. Du könntest das aber gegebenenfalls hier als entsprechende Frage einstellen. Und wenn ich oder jemand anderes das sieht, können wir dir helfen.
Ok alles gut, dann Versuche ich es so.
Habe es versucht mit dem Wurzelkriterium zu bestimmen und komme am Ende auf |z| < bzw. > 1/(lim n--->unendlich n-te√|an|) =: r wie mache ich von hier aus weiter. Bzw. Ist das überhaupt richtig? Hoffe du verstehst, was ich meine.
Kann ansonsten auch meine Lösung hochladen.
„und komme am Ende auf“
Von „am Ende“ kann da eher weniger die Rede sein. Das ist gerade mal der Anfang. Das ist nichts anderes als die sogenannte Formel von Cauchy-Hadamard:
https://de.wikipedia.org/wiki/Konvergenzradius#Bestimmung_des_Konvergenzradius
Die Formel kann man im Prinzip eigentlich immer nutzen, wenn man den Konvergenzradius berechnen möchte. Das ist richtig. Aber die Nennung dieser Formel reicht ja bei weitem nicht aus. Man muss das dann natürlich noch für den konkreten Fall berechnen... Und davon sehe ich bisher nichts von dir.
Wenn du deine Lösung mit mir/uns teilst, kann ich die auch gerne korrigieren.
Ansonsten habe ich dir in meiner Antwort schon entsprechende Hinweise gegeben, wie man die Aufgabe lösen kann, auf die du aber bislang nicht eingegangen bist. Falls du statt mit dem von mir genannten Quotientenkriterium deinen Ansatz mit dem Wurzelkriterium (also mit der Formel von Cauchy-Hadamard) weitermachen möchtest, kann ich dir noch den Hinweis geben:
Für die Fibonacci-Folge gibt es eine explizite Formel. Für nicht-negative reelle Zahlen a, b konvergiert außerdem die durch...
n-te Wurzel aus (a^n + b^n)
... gegebene Folge gegen max(a, b).
Meinst du an = 1/√5 (x1^n - x2^2); x1 = 1/2 (1+√5); x2 = 1/2 (1-√5) ?
Ja, genau. Diese explizite Formel meine ich. Die kann man in die Cauchy-Hadamard-Formel reinpacken, das dann berechnen/vereinfachen, um auf den gesuchten Konvergenzradius zu kommen.
bei b) bekomme ich z = (-1+-√5)/2
Nein. Wie bist du da auf diese Zahl gekommen? Da soll keine Zahl ausgerechnet werden.
Es geht bei Teilaufgabe b) um einen Beweis, den du aufschreiben sollst, dass f(z) = z/(1 - z - z²) für alle z mit |z| < r ist. Ein Beweis, keine Zahl als Ergebnis!
Ausmultiplizieren, dann mit einer Indexverschiebung die Exponenten der z-Potenzen angleichen, und dann (mit Hilfe von a[n+2] = a[n+1] + a[n]) die Koeffizienten vereinfachen, bis man merkt, dass nur noch z als einziger Summand übrig bleibt.
Wo sind deine Summen hin?
Ich habe dir jetzt einfach mal einen kompletten Lösungsvorschlag zu Teilaufgabe b) als Bild in meiner Antwort eingefügt, damit du siehst, was ich meine. Auch, wenn du dann Gefahr läufst, selbst zu wenig nachzudenken und einfach die Lösung zu übernehmen, wenn du nicht aufpasst.
Hey, danke erstmal für deine Hilfe. Könnte ich die privat meine Rechnung für die a) zeigen, komme gerade nicht so ganz weiter. Bzw. Ich weiß nicht, ob dass so richtig ist.