Kann man diese Aufgabe überhaupt so lösen?
"Ein Kompressor hat im ungefüllten Zustand bei 21 Grad Celsius Außentemperatur und einem Druck von 1.000 hPa eine Masse von 20,9 kg. Der Kompressorbehälter fasst 24 Liter. Nun wird der Behälter bis zu einem Überdruck von 7.000 hPa gefüllt. Was zeigt die Waage jetzt an? Die Dichte der Luft beträgt außerhalb des Kompressors 1,2 kg/m³ und der Kompressorbehälter hat sich nicht merklich erwärmt."
Kann man diese Aufgabe überhaupt mit den gegebenen Angaben berechnen? Ich konnte die Aufgabe zwar lösen, musste aber die molare Masse von Luft nachschauen, die war ja nicht in der Aufgabe gegeben. Könnte man die Aufgabe auch irgendwie anders Lösen, dass man nicht die molare Masse von Luft braucht?
4 Antworten
Der Geselle denkt kurz und arbeitet lange. Der Meister denkt lange und arbeitet kurz.
Also überlegen wir erstmal, was da eigentlich passiert. Wir holen aus der Umgebung ein bestimmtes Volumen an Luft und füllen das in den Vorratsbehälter. Genau die Masse dieser Außenluft zeigt die Waage anschließend mehr an.
Es ist völlig egal, ob ich das Außenluftvolumen per Kompressor in den Tank fülle oder ob ich anschließend den Behälter öffne und die Luft wieder rauslasse, um erneut den Anfangszustand zu erreichen. Das ändert nichts an der Masse der hin oder her strömenden Luftmasse.
Ideal ist auf jeden Fall, dass das ganze isotherm abläuft, also bei konstanter Temperatur. Das vereinfacht immer die Rechnung gewaltig, wenn man denn diese Tatsache für sich nutzt.
Wir gehen also vom Endzustand aus und da haben wir V = 24 l und p = 7 bar. Nun entspannnen wir das ganze isotherm auf 1 bar. Das berechnen wir mit dem Gesetz von Boyle-Mariotte. Für T = const. gilt:
p * V = const
p1/p2 = V2/V1
und lösen nach V2 auf:
V2 = V1 * p1/p2 = 24 l * 7/1 = 168 l
24 l waren und bleiben im Tank, also kommt aus der Umgebung das Luftvolumen Vl von:
Vl = 168 l - 24 l = 144 l = 0,144 m^3
Mit der gegebenen Dichte rechnen wir nun die Masse ml der Luft aus:
ml= ρ * V = 1,2 kg/m³ * 0,144 m^3 = 0,173 kg
Damit zeigt die Waage nun eine Masse m2 an:
m2 = m1 + ml = 20,9 kg + 0,173 kg = 21,073 kg
Danke! Mit deiner Antwort konnte ich es am besten nachvollziehen.
Oh ja, unbedingt. Das ist ein ganz typisches Fettnäpfchen, das gerne mal aufgestellt wird.
In die gleiche Kategoerie fallen Aufgaben, wie z.B. wieviel Liter Gas kommen bei konstanter Temperatur und 1 bar aus eine Flasche mit 200 bar und 1 l. Das sind nämlich nicht 200 l, sondern 199, weil die Flasche ja nicht bis zum Vakuum entleert wird , sondern 1 l bleibt in der Flasche zurück. Da muss man zwischen absolut und realtiv immer fein unterscheiden.
Würde dann, wenn man mit 8.000 hPa rechnet, eine Masse von 0,2304 kg hinzukommen?
Ich hab 0,202 kg raus.
V2 = V1 * 8/1 = 192 l
Abzgl. 24 l, kommen also 168 l dazu.
m = 0,168 m^3 * 1,2 kg/m^3 = 0,2016 kg
Ah, mist, habe am Ende statt 0,168 m^3 * 1,2 kg/m^3 0,192 m^3 * 1,2 kg/m^3 gerechnet, daher das falsche Ergebnis.
Ja. Man kann die Aufgabe mit den gegebenen Werten lösen, auch ohne die molare Masse von Luft kennen zu müssen.
Hier habe ich einen Rechenweg aufgeschrieben:
https://www.dropbox.com/s/4zwepy84bu6zzmw/Luft.pdf?dl=0
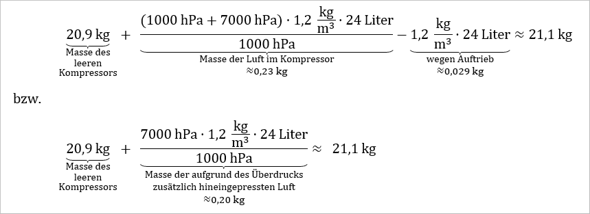
Letztendlich erhält man für die Masse des gefüllten Kompressors...

Bzw. wenn man die Auftriebskraft noch berücksichtigt, erhält man für den von der Waage angezeigten Wert...
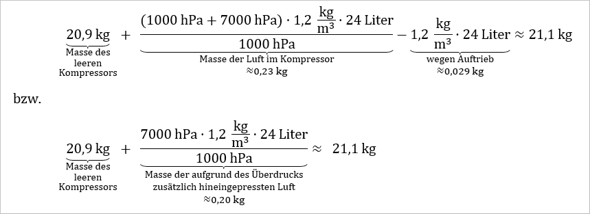
[Die Auftriebskraft fällt in diesem Fall quasi nicht ins Gewicht.]

Die Relation zur "fiktiven" Dichte der Luft war in der Aufgabenstellung durchaus gegeben :
Die Dichte der Luft beträgt außerhalb des Kompressors 1,2 kg/m³
Dabei wird sich die Aufgabenstellung auf einen Fiktivwert bei einem Luftdruck von 1000 hPa berufen.
Es geht nicht um die molare Masse , sondern um den Dichtewert gemäß Aufgabenstellung.
Ja, die dichte der Luft ist gegeben. Ich frage mich nur, ob das zur Berechnung dieser Aufgabe ausreicht oder ob nicht noch die Angabe der molaren Masse von Luft nötig gewesen wäre.
Für diese Aufgabenstellung ist genau die angegebene Luftdichte der richtige Lösungsansatz im Rechenweg . Die 1,2 KG/m3 beziehen sich dabei für die Aufgabenstellung auf einen Luftdruck von 1000 hPa .
Mit welcher Formel kommt man denn über die Dichte zum Ziel?
Ganz vereinfacht: 1 mol eines Gases nehmen 22,4 Liter ein. Nimm das mal als Ansatz (bei Normalbedingungen)
Aber wir habe eben keine Normalbedingungen, sondern einen Druck von 7.000 hPa.
Angeblich hast Du es über die molare Dichte doch bereits herausgefunden . Dann ersetze " molar " nun durch die 1,2 KG/m3 gemäß Aufgabenstellung
Überdruck bedeutet den Druckunterschied zwischen Umgebungsluft ( siehe Angabe in der Aufgabenstellung ) und .... hier halt 7000 hPa .
Kesselvolumen laut Aufgabe = 24 Liter
1m3 = 1000 Liter
Ich habe berechnet, dass in dem Gafäß 7,4012 mol sein müssen. Dass kann man doch nur mithilfe der molaren Masse in eine Masse umrechen, da hilft mir doch die Dichte nichts.
Es gilt pV=nRT. Wenn du das umstellt, hast du die Lösung
Genau die Formel habe ich ja auch verwendet am Ende bekomme ich 7,4012 mol raus. Um das in eine Masse umzurechen, bräuchte ich doch die molare Masse.
Bei 20 °C beträgt der Wert der Luftdichte nur noch rund 1,2041 kg/m3, Volumen hast du ja
Ja, ok. In welchem Zusammenhang steht das jetzt mit der Frage?
Du kannst doch mittels Dichte dann Volumen in Masse umrechnen
Ich weiß aber nicht die Dichte von Luft mit 7.000 hPa. Das ist in der Aufgabe nicht gegeben.
Mensch , in der Aufgabenstellung wurden doch 1,20 KG/m3 bei 1000 hPa angegeben . Wenn die da keine Koeffizienten und Mol haben wollen , rechnest Du ganz "stupide" mit diesen 1,20 KG/m3 × Überdruck in Relation zum Kesselvolumen.
Ab hier bin ich raus .
Schönes Wochenende .
Die Dichte bleibt doch m. W. Gleich.
Wessen Dichte? Die des Gases ist ziemlich stark vom Druck abhängig, Du erinnerst Dich an p * V = konstant?
Die ändert sich je nach Druck bei Gasen. Bei Flüssigkeiten ist das was anderes.
https://pawn.physik.uni-wuerzburg.de/video/thermodynamik/k/sk04.html
Nutz das mal als Ansatz
Habe die Aufgabe gerade nochmal durchgerechnet und mir nochmal deine Antwort nochmal angeschaut, um zu überprüfen, ob mein Ergebnis richtig ist. Mir ist jetzt aufgefallen, dass in der Aufgabestellung von einem Überdruck von 7.000 hPa gesprochen wird. Müsste man dann nicht eigentlich mit 8.000 hPa rechnen, da Überdruck ja bedeutet, dass in dem Behälter der Druck um 7.000 hPa höher ist als in der Umgebung, also 1.000 hPa+7.000 hPa=8.000 hPa?