Monotonie von Ordnungsrelationen?
Wie kann ich hier streng monoton fallend / streng monoton steigend beweisen?
(Auch den Unterschied zwischen streng und nicht streng)
Bei c) kann weder monoton fallend noch monoton steigend vorliegen, weil ja n1+1 ja nicht automatisch n2 + 1 teilt. (zB 2|4, aber nicht 3|5)
Danke
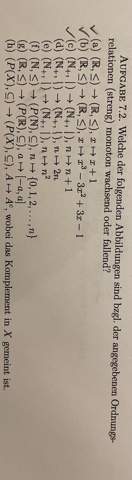
1 Antwort
In allen Aufgaben außer (b) wird die Monotonie der Funktion (nicht der Relation!) bewiesen, indem untersucht wird, ob die Definition der Monotonie erfüllt ist.
Ich beginne daher mit
(b)
Mit f(x) := x³ – 3x² + 3x – 1 gilt
f'(x) = 3x² – 6x + 3 = 3(x – 1)², also f'(x) = 0 ⇔ x = 1; sowie f'(x) > 0 für alle x ≠ 1.
Ferner ist f''(1) = 0 und f'''(1) ≠ 0, also hat f keine lokalen Minima oder Maxima, sondern lediglich bei x = 1 einen Sattelpunkt.
Aus alledem folgt, dass f streng monoton steigend ist. Unklar könnte allenfalls sein, was in der Nähe von x = 1 passiert. Betrachten wir dazu eine Zahl nahe bei 1: Wir können sie 1+d schreiben, mit winzigem positivem oder negativem d∈ℝ. Dann gilt f(1+d) = ... = d³ (nachrechnen!).
Also ist f(x) > 0 falls x > 1; f(x) = 0 falls x = 1; und f(x) < 0 falls x < 1. Die Abbildung f ist daher auch in der Nähe von x = 1 streng monoton.
Nun zu den übrigen Aufgaben. Für die darin angegebenen Funktionen untersuchen wir, ob sie die folgende Definition für "(streng) monoton" erfüllt:
Seien (M, R) und (N, S) geordnete Mengen. Eine Abbildung f: (M, R) → (N, S) zwischen geordneten Mengen (M, R) und (N, S) ist monoton, wenn für jedes x∈M und y∈N gilt:
x R y ⇒ f(x) S f(y).
f ist streng mononon , wenn für jedes x∈M und y∈N gilt:
x R y ∧ x ≠ y ⇒ f(x) S f(y) ∧ f(x) ≠ f(y).
(a)
Sei f(x) := x + 1. Dann gilt für x, y ∈ ℝ: x < y ⇒ f(x) = x + 1 < y + 1 = f(y).
Daher ist f streng monoton
(c)
Sei f(k) := k+1 und n, m ∈ ℕ+. Dann gilt:
n|m ⇒ ∃q∈ℕ+: q>1 ∧ m=qn ⇒ f(n) = n+1 < qn+1 = f(qn) = f(m).
Also ist f streng monoton.
(d)
Sei f(k) := 2k und n, m ∈ ℕ+. Dann gilt:
n|m ⇒ ∃q∈ℕ+: q>1 ∧ m=qn ⇒ f(n) = 2n < 2qn = f(qn) = f(m).
Also ist f streng monoton.
(e)
Sei f(k) := k² und n, m ∈ ℕ+. Dann gilt:
n|m ⇒ ∃q∈ℕ+: q>1 ∧ m=qn ⇒ f(n) = n² < q²n² = f(qn) = f(m).
Also ist f streng monoton.
(f)
Sei f(k) := {0, 1, 2, ..., k} und n, m ∈ ℕ+. Dann gilt:
n<m ⇒ f(n) = {0,1,2,...,n} ⊂ {0,1,2,...,n,n+1,...,m} = f(m).
Also ist f streng monoton. ("⊂" bedeutet echte Teilmenge).
(g)
Sei f(c) := [–c, c] und a, b ∈ ℝ. Dann gilt
falls 0 ≤ a < b: –a<a, –b<b, –b<–a und damit [–a, a] ⊂ [–b, b];
falls a < b ≤ 0: –a>a, –b>b, –b>–a und damit [–a, a] =⊘= [–b, b];
falls a < 0 < b: –a>a, –b<b, –b>–a und damit [–a, a] =⊘⊂ [–b, b].
Also ist f in allen 3 logisch möglichen Fällen monoton, aber wg. Fall 2 nicht streng monoton.
(g)
Sei f(M):=MC und A, B ∈ P(X). Dann gilt
A⊂B ⇒ f(B)=BC⊂AC=f(A).
Daher ist f nicht monoton, sondern antiton.