Kann mir bitte jemand bei der Aufgabe 9) weiterhelfen?

Hallo,

kann mir bitte jemand bei der Aufgabe 9) weiterhelfen? Ich weiß nicht wie man auf den Punkt D und S kommen soll, ich sitze seit 20 Minuten davor aber weiß nicht weiter. Mein Ansatz ist, dass der Vektor AB gleich dem Vektor CD sein müsste, aber weiter komme ich nicht...

Answer 1

[ProfFrink]

Mein Ansatz ist, dass der Vektor AB gleich dem Vektor CD sein müsste

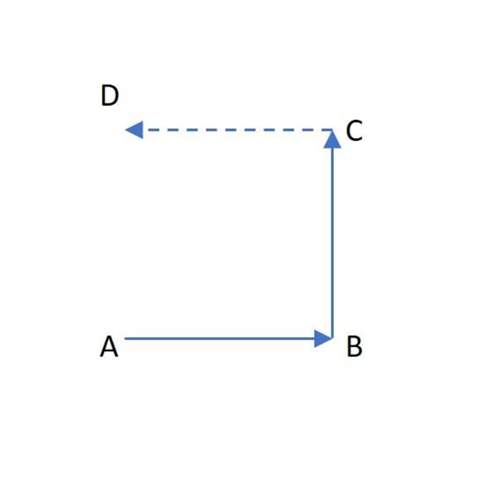
Die Vektoren AB und CD sind gleich, wenn Du die Subtraktion richtig vollzogen hast. Und sie sind an bestimmten Punkten fixiert, den Ortsvektoren mit ihren Koordinatenwerten. Schau Dir folgende Zeichnung an.

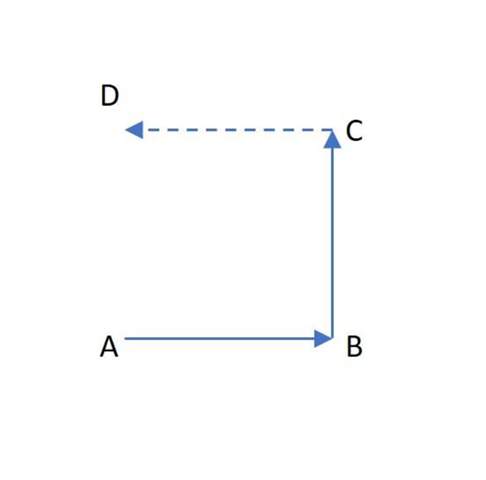
Du musst als nächstes Deinen Vektor einfach zum Ortsvektor C dazu addieren. Alternativ kannst Du auch den Vektor BC zum Ortsvektor A dazu addieren. Es muss der gleiche Punkt D erreicht werden. Eine gute Kontrollmöglichkeit.

Nachtrag:

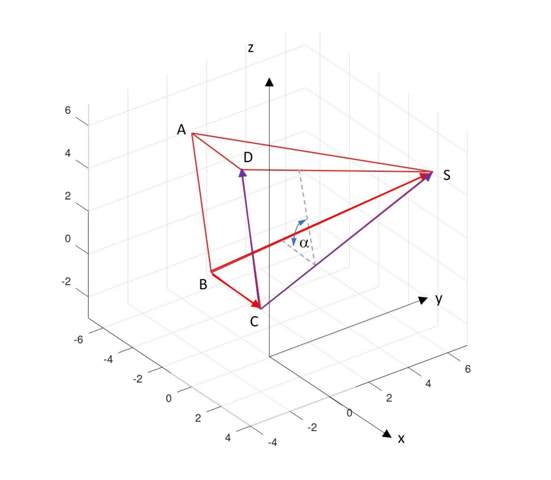
Rammstein53 hat Dir ja schon die nötigen Koordinaten ausgerechnet. Hier kommt die Lösung für die Teilaufgabe b) der Winkel zwischen benachbarten Seitenflächen. Erwartet wird hier ein Winkel zwischen 90° und 180°. Zur Orientierung ein Bild der Pyramide im Koordinatensystem und die Andeutung des interessierenden Winkels alpha.

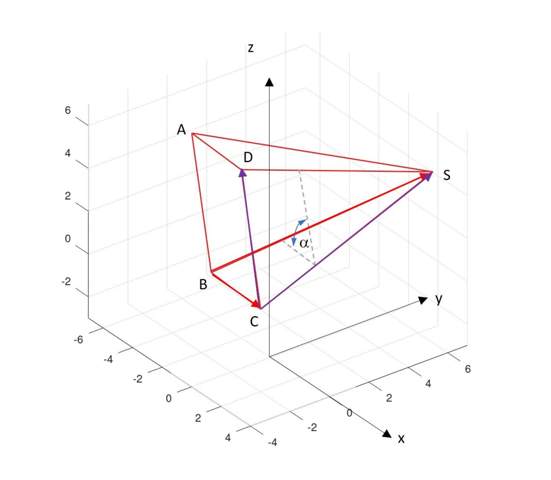
Der gesuchte Winkel kann über die Flächennormalenvektoren der Seitenflächen gewonnen werden. Über das Skalarprodukt kann der Winkel zwischen zwei Vektoren gewonnen werden. Die Normalenvektoren selbst werden wiederum aus zwei flächenaufspannenden Vektoren der Seitenflächen gewonnen. Die beteiligten Vektoren zur Berechnung der Normalenvektoren sind in rot und violett angedeutet. Hier die Fertigformel für alpha:

$\ \alpha=\arccos\frac{\left(\vec{BS}\ x\ \vec{BC}\right)\cdot\left(\vec{CD}\ x\ \vec{CS}\right)}{\mid\vec{BS}\ x\ \vec{BC}\left|\cdot\right|\vec{CD}\ x\ \vec{CS}\left|\right|}=95,7°$

Woher ich das weiß: Studium / Ausbildung

Answer 2

[Rammstein53]

A = (-4,-1,6), B = (0,-3,2), C = (-2,1,-2)

Abstand(A,B) = 6

Abstand(A,C) = 8.49

Abstand(B,C) = 6

A-B und B-C sind somit zwei Kanten der Pyramide, A-C ist eine Diagonale.

Um den Punkt D zu bestimmen, startet man z.B. bei A und geht in Richtung der Kante (C-B):

D = A + (C-B) = (-6, 3, 2)

Der Mittelpunkt der Grundfläche ergibt sich aus

M = (A+C)/2 = (-3,0,2)

Die Mittellinie der Pyramide steht senkrecht auf der Diagonalen A-C.

Diese Diagonale hat den Richtungsvektor A-C = (-2,-2,8). Ein dazu senkrechter Vektor ist z.B. (2,2,1).

Mittellinie m(t) = M + t*(2,2,1)

Der Betrag des Richtungsvektors soll 9 ergeben -> sqrt(4t² + 4t² + t²) = sqrt(9t²) = 9 -> t = 3.

S = m(3) = (-3,0,2) +3*(2,2,1) = (3,6,5)