Hilfe in Mathe?
Hi. könnt ihr mit bitte weiterhelfen?
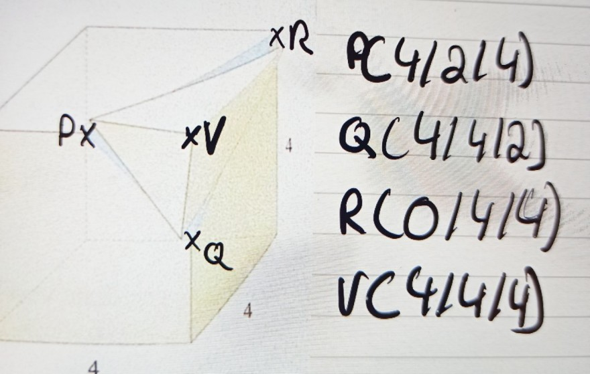
Von einem Würfel mit der Seitenlänge von 4m wurde eine Ecke wie dargestellt abgeschnitten.
a) Welche Höhe hat die Pyramide über der Schnittfläche?
b) Wie groß ist das Restvolumen des Würfels?
c) In welchem Punkt schneidet die Würfeldiagonale das blaue Dreieck?
LG
2 Antworten
a) Wenn wir die Fläche PQV als Grundfläche nehmen, spannen die Vektoren PQ und PV ein Parallelogramm auf, dessen Fläche dem Betrag des Kreuzproduktes dieser beiden Vektoren entspricht. Die Grundfläche der Pyramide ist dann die Hälfte davon.
PQ = Q - P = (4/4/2) - (4/2/4) = (0/2/-2)
PV = V - P = (4/4/4) - (4/2/4) = (0/2/0)
PQ x PV:
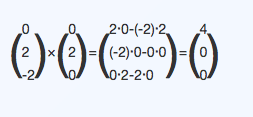

Damit beträgt die Gruzndfläche 4 FE (Flächeneinheiten)
Die Höhe der Pyramide entspricht dem Betrag des Vektors VR, da dieser senkrecht auf der Grundfläche steht.
VR = R - V = (0/4/4) - (4/4/4) = (-4/0/0)
Betrag von VR:

b)
Volumen der Pyramide:
V = 1/3 * G * h = 1/3 * 4 * 4 = 16/3 VE (Volumeneinheiten).
c) Der Würfel hat ein Volumen von:
V = 4 * 4 * 4 = 64
Restvolumen Vr:
Vr = 64 - 16/3 = 192/3 - 16/3 = 176/3 = 58 2/3
c)
Die Diagonale beginnt im Ursprung und geht durch V.
Gleichung der Diagonale:
Ortsvektor (0/0/0)
Richtungvektor OV:
OV = V - O = (4/4/4) - (0/0/0) = (4/4/4)
Damit hat die Diagonale die Gleichung:
g: x = (0/0/0) + r(4/4/4)
Die Schnittebene wird durch die Vektoren PQ und PR aufgespannt:

Nun schneiden wir g und E:


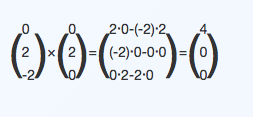





Ja, denn da ist ja nur nach der Höhe gefragt, allerdings nach der Höhe über der Schnittfläche, was mich immer noch verwirrt.
Aber die Punkte wurden so auch richtig ins Bild gezeichnet oder 😅?
Ja, die Punkte habe ich überprüft, die Stimmen, wenn der Ursprung hinten unten links ist.
Kannst du mir vlt im Bild einzeichnen welche Diagonale gemeint ist 😅
Von den 4 Diagoialen eines Würfels geht nur ein durch die Schnittfläche und das ist von Ursprung nach V. Alle anderen Diagonalen haben mit der Schnittfläche nichts zu tun.
Schaue dir die Formeln zur Berechnung von
- Abstand Punkt zu Ebene
- Volumen einer Pyramide
- Schnittpunkt Gerade mit Ebene
an und wende sie auf die Punkte aus der Aufgabe an. Für die b) kannst du eine beliebige Grundfläche und Höhe zur Berechnung des Pyramidenvolumens wählen.
Vielen lieben Dank!! Eine Frage wäre es bei a auch richtig wenn ich nur den 2. Teil aufschreibe also nur ab
Die Höhe der Pyramide entspricht dem Betrag des Vektors VR, da dieser senkrecht auf der Grundfläche steht.
VR = R - V = (0/4/4) - (4/4/4) = (-4/0/0)
Betrag von VR:
Oder ist der 1. Teil auch sehr wichtig?