Wie berechne ich diese Pyramide?
Aufgabe:
In einer quadratischen Pyramide ist der Diagonalschnitt ein gleichseitiges Dreieck mit der Seitenlänge 21,2cm. Berechne das Volumen der Pyramide und den Winkel zwischen der Seitenfläche und der Grundfläche.
Wie kann ich a und h Berechnen?
Vielen Dank im Voraus!
2 Antworten
Berechnung
h = Wurzel(s² - (d/2)²)
h = Wurzel(21,2^2 - 10,6^2)
h = 18,3597 rd. 18,36 cm
---
a = Wurzel(d² / 2)
a = Wurzel(21,2^2 / 2)
a = 14,991 rd. 15 cm
---
V = a² * h / 3
V = 15^2 * 18,36 / 3
V = 1377 cm³
---
α = arctan(h / (a/2))
α = arctan(18,36 / (15/2))
α = 67,792°
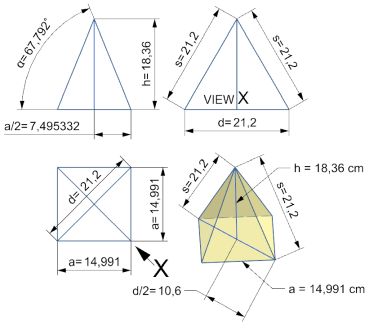
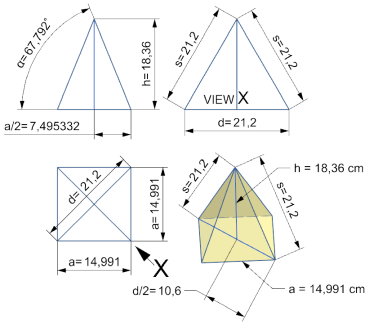
Fertigen Sie sich eine maßstäbliche Skizze an.
Dann sollten Ihnen die Zusammenhänge leicht ins Auge fallen.
Mit besten Grüßen
gregor443
Beim Diagonalschnitt bilden die Diagonale der Grundfläche und die Kantenlängen s der Pyramide das gleichseitige Dreieck.
Um die Seitenlänge der quadratischen Grundfläche zu bekommen, mußt Du s/Wurzel (2) rechnen.
Es ist ja ein gleichseitiges Dreieck, deshalb dachte ich a = 21,2cm um h zu berechnen habe ich die Wurzel von 22,2^2 - 10,6^2 gezogen. Da kam dann 18,36 raus. Dann habe ich damit das Volumen berechnet, das Ergebnis ist allerdings falsch.