Häufungspunkte von Folgen?
Hallo ich habe folgende Folge gegegeben :
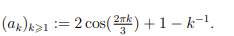
Ich soll die Häufungspunkte bestimmen indem ich Teilfolgen bilde und deren Grenzwerte betrachte.
Ich habe mir erstmal ein paar Punkte angeschaut und kann keine Häufungspunkte erkennen ? wie gehe ich vor?
4 Antworten
Der cos ist eine Funktion mit der Periode 2*pi. Das Maximum des cos(x) liegt bei 1 . Immer wenn der cos(x) bei k = 3n sein Maximum erreicht hat ergibt sich ak = 2 + 1 - k^(-1). Je größer k wird, desto mehr nähert sich k^(-1) der Zahl Null. Also ist 3 ein Häufungspunkt der Folge.
Ja, denn k kann nur die Werte k = 3n ; k= 3n-1 und k = 3n-2 für n aus |N und n >0 annehmen.
Der Term 1/k spielt keine Rolle, weil er gegen Null konvergiert.
cos ( 2*pi*k/3) = -1/2 für k = n*3+1,n*3+2
cos ( 2*pi*k/3) = +1 für k = n*3
daraus folgt
2*cos ( 2*pi*k/3) = -1 für k = n*3+1,n*3+2
2*cos ( 2*pi*k/3) = +2 für k = n*3
daraus folgt
2*cos ( 2*pi*k/3) + 1 = 0 für k = n*3+1,n*3+2
2*cos ( 2*pi*k/3) + 1 = +3 für k = n*3
Die Folge hat somit die Häufungspunkte 0 und 3.
Schau dir erstmal die Folge
cos(2pi k/3) an.
Siehst du die Häufungspunkte davon? Kannst du das beweisen?
Schlussfolgere daraus, was die Häufungspunkte von
2 cos(2pi k/3) + 1
sind.
Welche Teilfolgen der natürlichen Zahlen korrespondieren zu diesen Häufungspunkten?
Schau dir für diese Teilfolgen dann
2 cos(2pi k/3) + 1 - k^-1
an. Konvergiert das auf den jeweiligen Teilfolgen?
Zum beispiel k gerade oder k ungerade?
k ist ja eine natürliche Zahl...
Vielleicht hilft das...
Bedenke: Der Grenzwert einer konvergenten Folge ist ihr einziger Häufungspunkt.
ich habe das jetzt so gemacht :
habe k = 3j mit j>0 gewählt , was also zB 3,6,9 ist.
habe für k also 3j eingesetzt und j gegen unendlich laufen lassen wobei rauskam 3.
Ist 3 also ein Häufungspunkt?
und muss ich das gleiche jetzt noch für 3j+1 und 3j+2 machen ? und habe ich dann garantiert alle Häufungspunkte ?
ja , also es gilt ja das cos(2pi*k/3) für k = 1 und k = 4 usw gleich ist ? weil cos ja periodisch ist.
also wäre es ja sinnvoll für k einmal 3j , einmal 3j+1 und einmal 3j+2 anzuschauen oder ?
ja , also es gilt ja das cos(2pi*k/3) für k = 1 und k = 4 usw gleich ist ? weil cos ja periodisch ist.
also wäre es ja sinnvoll für k einmal 3j , einmal 3j+1 und einmal 3j+2 anzuschauen oder ?
für k = 3j habe ich schon den limes berechnet nämlich 3 , wie du auch gesagt hast, aber wenn ich das so mache habe ich denn dann sicher alle ?