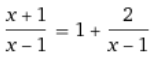Grenzwert gegen Unendlich ermitteln?
Hallo
Ich möchte den Grenzwert im Positiven gegen unendlich für die Funktion
ln((x+1)/(x-1))/(1/x)
ermitteln
Also Lim x gegen unedlich
Ich verstehe leider nicht wie ich rechnerisch, bei der Grenzwertbestimmung, vorgehen muss.
5 Antworten
Betrachte zunächst das Argument des Logarithmus:
(x+1)/(x - 1) = 1 + 2/(x - 1) wobei 2/(x - 1) --> 0 für x --> inf
Wir entwickeln also nun ln(1 + x) in x = 0, und erhalten:
ln(1 + x) = ln(1) + 1/(1 + 0)*(x - 0) - 1/(2*(1 + 0)²)*(x - 0)² + O(x^3)
(Taylor-Entwicklung bist zweiter Ordnung)
Einsetzen liefert nun:
ln(1 + 2/(x - 1)) = (2/(x - 1)) - (2/(x - 1))²/2 + O((1/x)^3)
Somit können wir die Gesamtfunktion für x --> inf approximieren durch:
ln((x+1)/(x-1))/(1/x) = ln(1 + 2/(x - 1))*x
= (2/(x - 1)) - (2/(x - 1))²/2 + O((1/x)^3)*x
= 2x/(x - 1) + O(1/x) = 2/(1 - 1/x) + O(1/x) ---> 2 für x --> inf
Somit erhalten wir also insgesamt:
lim(x->inf){ ln((x+1)/(x-1))/(1/x) } = 2
https://www.mathebibel.de/regel-von-lhospital
ich denke aber, dass l'hospital hier nicht greift.
Der grenzwert ist bei deiner funktion 2
setz für x dann 1000 ein; dann siehst du es.
Vielleicht weiß jemand hier, wie man rechnerisch auf die 2 kommt.
wieso , das greift doch gleich beim ersten Mal:
d/dx (ln(...) = -2/(x²-1)
d/dx 1/x = -1/x²
der Quotient der beiden Ausdrücke ist im Limes 2.
Wenn Du hier die Grenzwerte vom Zähler (ln) und vom Nenner (1/x) einzeln berechnest, kommt 0/0 raus, d. h. hier kommt die Regel von l'Hospital zum Einsatz, d. h. Zähler und Nenner jeweils für sich ableiten, dann nochmal die Grenzwertberechnung probieren. Dann sollte es funktionieren (es sollte 2 rauskommen...)
ln((x+1)/(x-1))/(1/x) kannst du umstellen zu
x * ln(x+1/x-1) (durch einen Bruch teilen, indem man mit dem "Kehrwehrt" multipliziert)
, dann wird relativ schnell klar, dass beim Einsetzen größerer Zahlen für x bei ln(x+1/x-1) immer ein Ausdruck der Form 0,00000(..)0001999.. herauskommt. Wenn man also unendlich einsetzt, strebt der Funktionswert gegen 2
Man kann auch
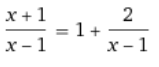
schreiben. Daher ergibt der Grenzwert 2, da