Gibt es eine Funktion, die punktsymmetrisch ist, aber nicht durch den Ursprung (0/0) verläuft?

Gibt es eine Funktion, die punktsymmetrisch ist, aber nicht durch den Ursprung (0/0) verläuft?

oder alles was punktsymmetrisch ist, muss durch (0/0) verlaufen?

Answer 1

[mihisu]

Klar gibt es solche Funktionen. Beispielsweise die folgende Funktion:

============

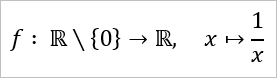
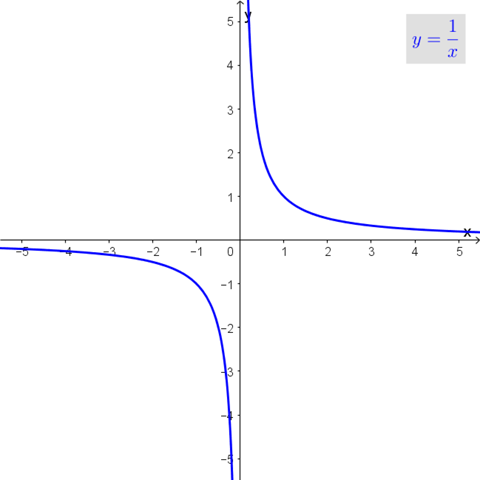
Wenn allerdings 0 im Definitionsbereich liegen soll, so muss der entsprechende Funktionswert gleich 0 sein, also die Funktion durch den Punkt (0 | 0) verlaufen.

Denn dann muss wegen der Bedingung f(-x) = -f(x) für alle x insbesondere f(-0) = -f(0) sein.

$f\left(-0\right)=-f\left(0\right)$ $\Leftrightarrow\ \ f\left(0\right)=-f\left(0\right)$ $\Leftrightarrow\ \ 2\cdot f\left(0\right)=0$ $\Leftrightarrow\ \ f\left(0\right)=0$

Es gibt aber auch ungerade Funktionen (also Funktionen deren Graph punktsymmetrisch zum Ursprung verläuft), welche nicht durch den Punkt (0 | 0) verlaufen. Dann ist allerdings 0 nicht im Definitionsbereich.

Comments

[mihisu]

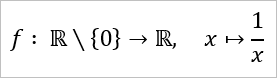
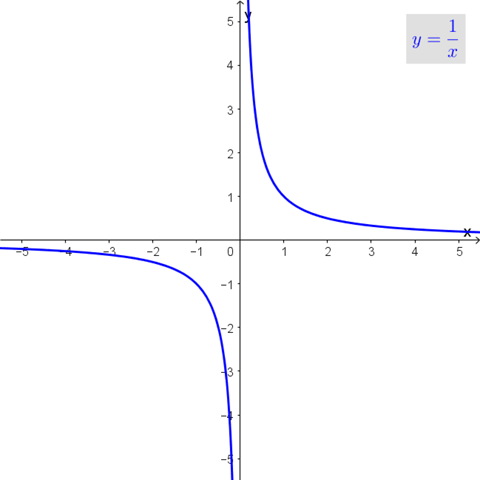
Andererseits hast du gar nicht gefordert, dass die Funktion punktsymmetrisch zum Ursprung verlaufen soll, sondern nur, dass sie punktsymmetrisch verlaufen soll.

Demnach wäre beispielsweise durch
f: ℝ → ℝ, x ↦ x + 1
eine Funktion gegeben, deren Graph punktsymmetrisch ist, nämlich beispielsweise punktsymmetrisch zum Punkt (0 | 1).
Die Funktion verläuft dann wegen f(0) = 0 + 1 = 1 ≠ 0 nicht durch den Punkt (0 | 0).
Skizze: https://i.imgur.com/TcjfGYD.png

Answer 2

[Tyldu]

natürlich. da gibts unzählige.

$f_{\left(x\right)}=\ \frac{1}{x}$ wäre davon beispielsweise schon eine. ist punktsymmetrisch zum ursprung, und sogar nicht definitiert für x=0 und y=0

Answer 3

[Arkan2k2]

(X^3) +1

Ist punktsymmetrisch zu 0/1 , aber verläuft nicht durch 0/0