Gegeben sind ein Punkt auf der Parabel und die unvollständige Parabelgelichung?
(1) P(-1|7,5) f(x)= x^2 + px +2,5 Also aufjedenfall mit der Pq Formel lösbar aber wie genau?
6 Antworten
Erst einmal brauchen wir eine Aufgabe.
Ich vermute, dass die Aufgabe ist, die Funktion zu vervollständigen, richtig?
Fassen wir nochmal zusammen:
f(x) = x² + px + 2,5
Der Punkt P(-1|7,5) liegt auf der Funktion.
Um die Funktion nun zu vervollständigen, brauchst du die pq-Formel nicht! Die pq-Formel kannst du anschließend aber noch nutzen, um die Nullstellen zu berechnen.
Du kannst aus dem Punkt eine mathematische Bedingung machen und anschließend die Gleichung auflösen.
Das geht so:
f(x) = x² + px + 2,5
P(-1|7,5)
Die Mathematische Bedingung:
f(-1) = 7,5
Das packen wir nun in die Funktion. Das heißt, wir setzten für x=-1 rein. Rauskommen muss am Ende 7,5. Also wird aus f(-1) dann 7,5. Anschließend lösen wir nach p auf.
f(x) = x² + px + 2,5
f(-1) = 7,5
7,5 = (-1)² + p*-1 + 2,5
7,5 = 1 - p + 2,5 |-1
6,5 = - p + 2,5 |-2,5
4 = - p | : -(1)
p = -4
Dieses Ergebnis setzen wir nun in die Funktion ein:
►► f(x) = x² - 4x + 2,5
● ● ● Probe ● ● ●
Wir setzen den berechneten Wert nun in die Funktion ein und prüfen, ob der Punkt tatsächlich auf der Funktion liegt. Wir machen also fast das selbe wie vorhin und setzen die Werte ein. Rauskommen muss f(-1)= 7,5.
f(x) = x² + px + 2,5
p = -4
f(x) = x² - 4x + 2,5
P(-1|7,5)
f(-1) = (-1)² - 4*(-1) + 2,5
f(-1) = 1 + 4 + 2,5
f(-1) = 7,5
► Das heißt, der Punkt P(-1|7,5) liegt tatsächlich auf der Funktion f.
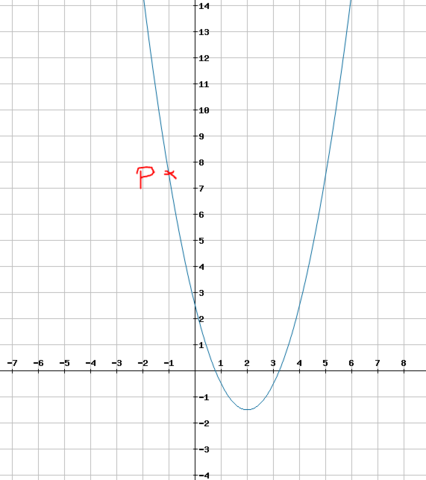
Im Bild siehst du die berechnete Funktion nochmal! :)
__________________________________________________________
Nun kannst du auch die Nullstellen der Funktion mit der pq-Formel berechnen. Da kommen übrigens 2 Lösungen raus, die sehr blöde Dezimalzahlen sind. Wundere dich darüber also nicht.
__________________________________________________________
Bei Fragen oder Anregungen einfach melden! :)
Liebe Grüße
TechnikSpezi
Du setzt einfach den Punkt ein, dann bleibt p als Unbekannte übrig; pq-Formel ist also nicht nötig...
f(x) = x² + px + 2.5
und
P = (-1 | 7.5)
Einsetzen in unsere Gleichung liefert:
7.5 = f(-1) = 1 - p + 2.5 II - 3.5
4 = - p II *(-1)
p = -4
Wir erhalten somit für die Funktionsgleichung:
f(x) = x² - 4x + 2.5
1 - p + 2,5 = 7,5 wenn man x und y einsetzt
-p = 4
p = -4
=> f(x) = x² - 4x + 2,5
Schneller geht's nicht.
Du setzt x und y des Punktes ein und stellst nach p um:
7,5 = (-1)² + p * (-1) + 2,5