Exponentielle Abnahme?

Wie muss ich das ausrechnen? Bzw wie sieht die Funktion dafür aus

Answer 1

[fragenhelfer888]

Als Erstes muss eine Funktionsgleichung aufgestellt werden. Dazu folgende Gedanken:

Anfang November besitzt der Eichenbaum 100% an Laubwerk. Im Januar sind davon nur noch 62% vorhanden. 2 Monate später werden nur noch 38,44% (0,62*0,62) vorhanden sein usw. Es ist charakteristisch für exponentielles Wachstum, dass sich ein Bestand im selben Zeitintervall immer um einen konstanten Faktor verändert.

Exponentielle Gleichungen besitzen die Form

$y\left(x\right)=a^x$ dabei bezeichnet y eine Größe, die von x abhängt, a ist eine bestimmte Basis und x steht im Exponenten.

Für die Aufgabe wählen wir als Bezeichnung N für den Laubbestand und t für die Zeit. Dabei muss man sich auf eine Einheit einigen, hier sollen es Monate sein. Die Basis a kennen wir noch nicht. Die Funktionsgleichung könnte dann etwa so aussehen:

$N\left(t\right)=100\%\cdot a^t$ Die Basis kann man berechnen, wenn man die Information aus der Aufgabe einsetzt. Wir wissen, dass der Bestand nach 2 Monaten nur noch bei 62% liegt.

$62\%=100\%\cdot a^2$ Diese Gleichung nach a auflösen.

$62\%=100\%\cdot a^2$ $0,62=a^2$ $a=\sqrt{0,62}$ Die Funktionsgleichung sieht also folgendermaßen aus:

$N\left(t\right)=100\%\cdot\sqrt{0,62}^t$

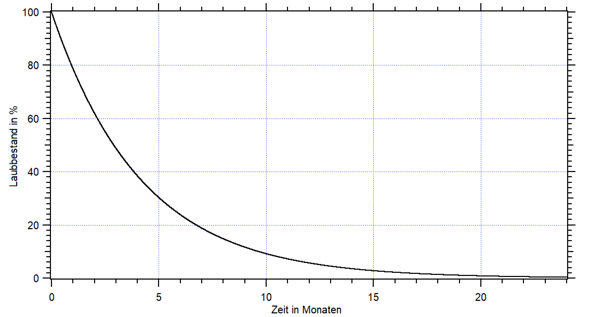
Veranschaulicht:

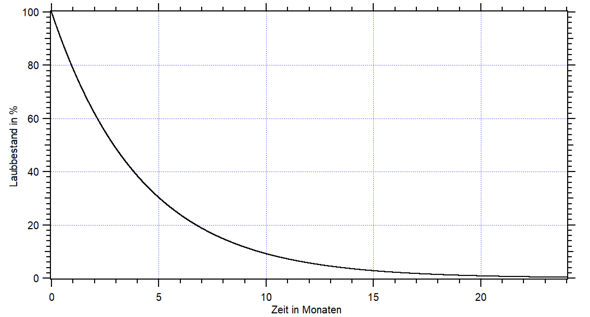
Nun schaut man sich an, wie viele Monate es bis zu den geforderten Zeiten sind (von November aus).

Bis zum Februar sind es 3 Monate.

Bis zum Mai 6 Monate.

Bis zum Juli 8 Monate.

Diese Zahlen setzt man in die Funktionsgleichung für t ein und man erhält den Laubbestand zu der Zeit.

$N\left(3\right)=100\%\cdot\sqrt{0,62}^3\approx48,82\%$ $N\left(6\right)=100\%\cdot\sqrt{0,62}^6\approx23,83\%$ $N\left(8\right)=100\%\cdot\sqrt{0,62}^8\approx14,78\%$

Comments

[Fragen200021]

Danke dass du dir die Mühe machst!!⭐⭐

[fragenhelfer888]

@Fragen200021

Freut mich, wenn ich helfen kann. ✌

Answer 2

[FaulesStueck]

januar sind 2 monate, also ist x²=0,62

x ist dann 0,79

die funktion ist y=0,79x hoch n

n sind die monate

Comments

[fragenhelfer888]

Dann sollte man für die Basis x aber auch anstatt 0,79 direkt √0,62 verwenden (was grob gerundet 0,79 ergibt). Nach 8 Monaten (November-Juli) ergäbe sich dadurch ein Fehler von etwa 2,7%. Noch 2 Jahre später läge der Fehler dann schon bei 11%. Runden nur ganz zum Schluss.

[FaulesStueck]

@fragenhelfer888

ok

[Fragen200021]

Danke!

Answer 3

[Geograph]

Manchmal möchte man verzweifeln:

Was ist das wieder einmal für eine bescheuerte Aufgabenstellung aus der "Praxis"

Eine Eiche trägt also im Hochsommer (Juli) neben den diesjährigen Blättern auch noch 15% des (inzwischen vertrockneten) Laubes vom Vorjahr.

Da hat der Aufgabensteller in seiner Schulzeit in Biologie wohl längere Zeit gefehlt.

Comments

[Geograph]

Nicht vergessen:

Dazu kommen auch noch 0,8% des Laubes vom vorvorigen Jahres (:-(((