einen beweis in mathe durchführen?
hi leute, ich muss in mathe einen beweis vorführen und zwar den Peripheriewinkelsatz. Aber irgendwie verstehe ich den nicht. Der Satz lautet: " Wenn zwei Peripheriewinkel über demselben Bogen liegen, dann sind diese Winkel gleich groß. " Kann mir jemand weiterhelfen?? (Es ist keiin Schummeln oder so, wenn ich euch frage, denn wir dürfen uns Hilfe holen) Wäre euch echt dankbar für Antworten Danke im Vorraus lg:)
1 Antwort
Hallo,
da alle Peripheriewinkel über demselben Bogen denselben Zentriwinkel haben und der Zentriwinkel immer doppelt so groß ist wie die Peripheriewinkel über demselben Bogen, müssen diese Peripheriewinkel alle die gleiche Größe haben.
Das ist einfach zu beweisen.
Dazu mußt Du allerdings auch beweisen, daß Peripheriewinkel wirklich halb so groß sind wie dazugehörige Zentriwinkel - und das geht so:
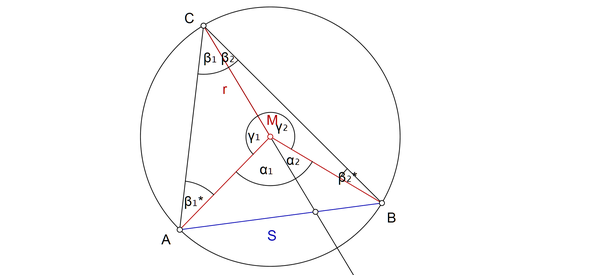
Betrachte die Zeichnung, die ich Dir hochlade:
Du siehst einen Kreis mit einer Sehne S, die die Punkte A und B verbindet.
Beide Punkte sind einmal mit dem Mittelpunkt M verbunden, so daß Du den Zentriwinkel AMB erhältst, außerdem mit dem Punkt C, so daß Du den Peripheriewinkel ACB erhältst.
Nun gibt es einen Strahl, der von Punkt C ausgehend durch Punkt M geht und den Peripheriewinkel in die beiden Winkel β₁ und β₂, sowie den Zentriwinkel in die beiden Winkel α₁ und α₂ aufteilt.
Dabei bilden die Kreisradien r von M nach A und von M nach C das gleichschenklige Dreieck ACM mit den zwei gleichen Winkeln β₁.
Der Winkel γ₁ nun hat die Größe 180°-2β₁.
Der Winkel α₁ hat die Größe 180°-γ₁ oder 180°-(180°-2β₁)=2β₁.
Entsprechendes gilt für das Dreieck BCM mit den Winkeln β₂, γ₂ und α₂.
α₂ hat somit die Größe 2β₂.
Somit gilt: α₁+α₂=2(β₁+β₂)
Da aber α₁+α₂ den Zentriwinkel AMB bilden und β₁+β₂ den Peripheriewinkel ACB, gilt: Winkel AMB=2*Winkel ACB.
Herzliche Grüße,
Willy