Mathe Aufgabe Sehne des Kreises?

Zeichne eine Strecke AB der angegebenen Länge. Konstruiere dann einen Kreis mit AB als Sehne so, dass die Peripheriewinkel über dem Bogen AB die Größe Gamma besitzen.

AB = 4,8cm; Gamma = 70°

Ich sitz schon 3 Stunden an der Aufgabe und weiß nicht wie ich die lösen soll

Danke im Voraus

Answer 1

[jeanyfan]

Dazu musst du den Umfangwinkel-Satz kennen, der dir besagt, dass der Winkel am Mittelpunkt M des Dreiecks ABM doppelt so groß ist wie der Peripheriewinkel bei C auf der Kreislinie:

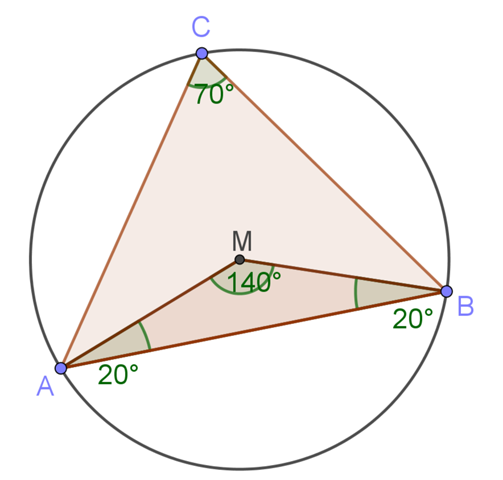
Das Dreieck ABM hat also den doppelten Peripheriewinkel 2*70°=140° bei M und da es gleichschenklig ist (AM und BM entsprechen beide dem Kreisradius) sind die Winkel bei A und B jeweils 20°.

Zunächst zeichnest du also AB als Strecke und an beiden Eckpunkten im Winkel 20° Geraden, die sich in M schneiden. Dann kannst du um M einen Kreis mit Radius AM=BM zeichnen. Und einen beliebigen Punkt als C auf der Kreislinie wählen und daraus das Dreieck ABC verbinden.

Comments

[MohiHa]

Vielen Dank

Kuss

[jeanyfan]

@MohiHa

Mit dem Umfangwinkel-Satz ist es einfach. Aber ohne den bist du hier aufgeschmissen. Ging mir auch so, als ich solche Aufgaben lösen wollte und nicht wusste, dass ich den dafür brauche.

Answer 2

[Ellejolka]

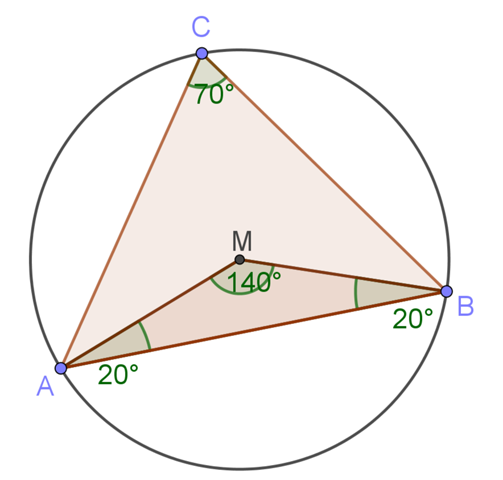
Du weißt, dass dann der Mittelpunktswinkel 140° haben muss?

Zeichne eine Waagerechte Strecke AB und halbiere sie. Durch die Mitte zeichnest du eine Senkrechte zu AB. Auf der Senkrechten suchst du den Punkt, der den Winkel 140° ergibt. Das ist dann der Mittelpunkt des Kreises. usw