ABCD sei ein Sehnenviereck. Beweisen Sie, dass die jeweils gegenüberliegenden Winkel im Viereck zusammen 180 Grad ergeben?
ABCD sei ein Sehnenviereck. Beweisen Sie, dass die jeweils gegenüberliegenden Winkel im Viereck zusammen 180 Grad ergeben. Wie kann man das beweisen? Mit dem Satz des Thales?

2 Antworten
Der Satz des Thales kann hier zumindest nicht direkt angewandt werden, da er erfordert, dass deine Grundseite durch den Kreismittelpunkt läuft. Es ist deutlich leichter, als es aussieht.
Spoiler:
Je nachdem wie viel ihr schon bewiesen habt:
Mithilfe einfacher geometrischer Konstruktionen beweist man, dass ein Dreieck immer die Innenwinkelsumme von 180° hat. Eine Referenz dazu findet man beispielsweise hier:
https://math.stackexchange.com/a/269852
Die vier Winkel in der Mitte bilden offenbar in Summe den Vollwinkel 360°.
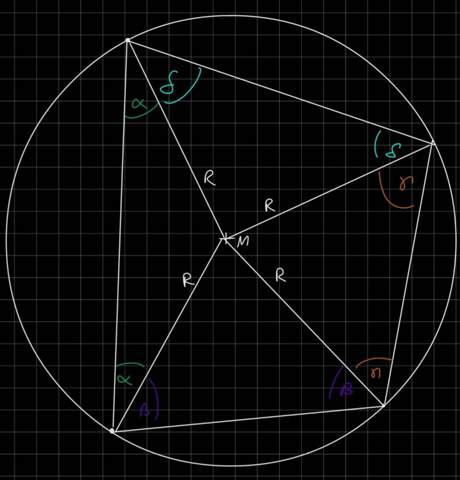
Die hier gezeigte Winkelaufteilung ist nicht hilfreich. Teile stattdessen dein Viereck in jene vier Dreiecke auf, die durch die Verbindung des Kreismittelpunktes mit den vier Eckpunkten entstehen. Du bekommst jeweils wegen des Radius gleichschenkelige Dreiecke, mit gleichen Basiswinkeln. Diese haben jetzt eine ähnliche Aufteilung wie oben, und es ergibt sich erneut
2*(a+b+c+d)+360°=4*180° -> a+b+c+d=180°, was zu zeigen war. [Übersetze in alpha, beta, gamma, delta]

Es gibt 4 gleichschenklige Dreiecke, im Dreieck beträgt die Winkelsumme 180°, deshalb rechts des Gleichheitszeichens 4*180°.
Da jedes der vier Dreiecke gleichschenklig ist, tauchen die Winkel an den Schenkeln, also a, b, c und d, in dieser Summe je zweimal auf, das macht 2*(a+b+c+d) auf der linken Seite. Weil die vier dabei noch unberücksichtigten Winkel um den Kreismittelpunkt zusammenliegen, ergänzen sie sich zu 360°. Deshalb steht auf der linken Seite 2*(a+b+c+d) + 360°, das sind also auch die Winkelsummen der vier Dreiecke, dort aber mit Berücksichtigung ihrer Gleichschenkligkeit.
4*180, weil du vier Dreiecke hast. Davon bilden die vier Winkel in der Mitte einen Vollwinkel. Die anderen Winkel sind je zwei mal dabei, also
Gesamte Winkel in den Dreiecken = 4*180 = 360+2(a+b+c+d) = All die einzelnen Winkel
Das würde für jedes Viereck gelten, nicht nur für ein Sehnenviereck. Gilt die Aussage für jedes Viereck? Glaube nicht.
M.m.n. garantiert die Eigenschaft des Sehnenvierecks jene Aufteilung der Winkel. Nur mit dieser Aufteilung der Winkel funktioniert meine Argumentation, also ist mein Beweis sinnvoll.
Nunja, da dieses Bild beigefügt wurde, dachte ich, dass das verwendet werden darf. Ich füge den Beweis an.
Ich glaube, dass es wirklich bedeutsam ist, welche Sätze bereits gegeben sind.
Nein, man braucht die Winkelaufteilung gar nicht. Es ist immernoch sehr einfach. Gib mir zwei Minuten.
Die Aussage, dass die gegenüberliegenden Winkel in Summe 180° ergeben, gilt im Sehnenviereck, aber im allgemeinen Viereck nicht. Das bedeutet, dass jeder Beweisversuch, in dessen Argumentation die Eigenschaft des Sehnenvierecks nicht einfließt, nicht korrekt sein kann.
Ich finde es nicht trivial. Mit dem Kreiswinkelsatz ist es trivial, aber der muss bekannt sein, oder zuerst bewiesen werden.
Den brauchst du nicht. ChatGPT hat noch keine gute geometrische Intuition. Wenn man ein paar geometrische Beweise kennt, fühlt man hier intuitiv, dass der Beweis nicht schwer sein kann. Siehe meine bearbeitete Antwort.
Ich bin übrigens auch nur so schnell darauf gekommen, weil ich ein Sehnenviereck als Bild gegoogelt habe, und dort diese viel bessere Aufteilung gezeigt wurde.
alpha, beta, gamme, delta...
Ich habe keine griechische Tastatur. Das sollte doch Recht offensichtlich sein :D
Genau, b ist beta, c ist gamma, d ist delta. So identifiziert man sie ja normalerweise.
Glaube ich auch nicht, aber hier wird ausgenutzt, dass die Lage der 4 Ecken auf dem Kreis zu gleichschenkligen Dreiecken führt. (OK, habe erst jetzt die anderen Kommentare gesehen ....)
Hängt davon ab, welche bewiesenen Sätze schon zur Verfügung stehen.
Hier ist, was ChatGPT dazu einfällt:
Beweis
Gegeben: Ein Sehnenviereck ABCD dessen Eckpunkte A, B, C, und D auf einem Kreis liegen.
Behauptung: ∠A+∠C=180° und ∠B+∠D=180°
Beweisidee: Wir nutzen den Kreiswinkelsatz, der besagt, dass ein Winkel, der über einen Kreisbogen am Umfang des Kreises gebildet wird, gleich der Hälfte des Zentriwinkels über demselben Bogen ist.
Betrachte die gegenüberliegenden Winkel ∠A und ∠C im Sehnenviereck.
- ∠A wird durch den Kreisbogen BCD aufgespannt.
- ∠C wird durch den Kreisbogen DAB aufgespannt.
Der gesamte Kreis wird durch die Bögen BCD und DAB vollständig abgedeckt. Der Zentriwinkel über BCD plus der Zentriwinkel über DAB ergibt 360°.
Nach dem Kreiswinkelsatz:
- ∠A=1/2⋅ (Zentriwinkel über Bogen BCD),
- ∠C=1/2⋅ (Zentriwinkel über Bogen DAB).
Da die Summe der Zentriwinkel über BCD und DAB 360° beträgt:
Zentriwinkel über BCD + Zentriwinkel über DAB=360°.
Daraus folgt für die gegenüberliegenden Winkel: ∠A+∠C=1/2⋅360°=180°
Ein analoges Argument gilt für die Winkel ∠B und ∠D.
Fazit: Die gegenüberliegenden Winkel eines Sehnenvierecks ergeben zusammen 180°.
q.e.d.
Aber dazu müsste der Kreiswinkelsatz bereits bekannt sein.
Vielen Dank.
Uns wurde gesagt, wir sollen den Satz des Thales bzw. Umfangwinkelsatz anwenden.
Ich glaube, der Kreiswinkelsatz ist der Umfangwinkelsatz. Der Satz ist Thales ist dessen Spezialisierung, wenn der Zentriwinkel gestreckt ist, also 180° hat.
Man kann dann sagen: Die Winkel bei B und D sind beide Umfangwinkel für die Punkte A und D. Da B und D auf unterschiedlichen Seiten der Strecke AC liegen, ergänzen sich ihre Zentriwinkel zu 360°, also entspricht die Summe ihrer selbst als Umfangwinkel der Hälfte davon, also 180°. Mit analogem Schluss für die Winkel bei A und D folgt die Behauptung.
Ich verstehe nicht genau wieso das so formuiert wurde „2*(a+b+c+d)+360°=4*180° -> a+b+c+d=180°“.
Also warum ist 360 Gard zu den Winkeln addiert?