E Funktionen miteinader teilen?
Guten Abend!
Ich habe gerade eine Aufgabe berechnet und da kam ich zu einem punkt an dem ich nicht mehr weiter weiß.
Also ich weiß nicht wie ich die beiden e funktionen teilen kann bzw. welche Regeln ich da beachten muss.
Mir ist klar, dass sich die 10 wegkürzt, doch ich weiß nicht wie ich die Zahlen über e in Beziehung zu setzen soll, also was jetzt wie miteinader zusammengerechnet wird.
Ich hoffe Ihr könnt mir helfen - ich möchte nicht das Ergebnis, sondern nur die Erklärung wie ich vorgehen muss bzw. in welcher Reihenfolge ich was beachten muss.
Vielen Dank im voraus
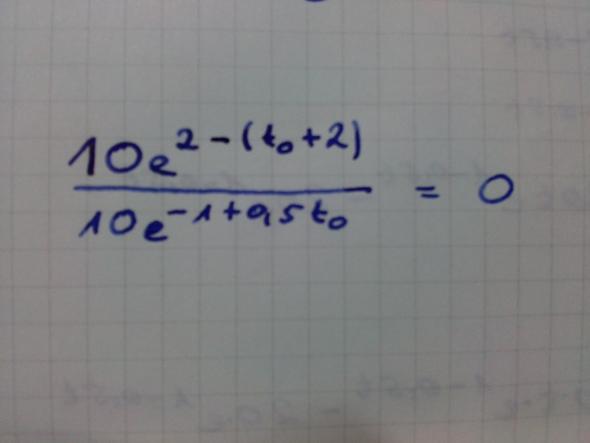
3 Antworten
Du hast hier eine Gleichung, und zwar einen Bruchterm, der gleich 0 sein soll.
Betrachte mal das hier:
a/b = 0 | mal b und gleich kürzen
a = 0
Du musst nur den Zähler gleich 0 setzen. Ein Bruch bzw ein Bruchterm ist gleich 0 genau dann, wenn der Zähler gleich 0 ist (wobei der Nenner natürlich nie 0 sein darf; aber dein Nenner wird ja auch nicht 0)
bleibt nur nur das e hoch...
Genau. Und dann brauchst du nicht mehr weiter zurechnen. Denn "e hoch irgendwas" wird nie 0. Also, die Lösungsmenge ist leer.
Wenn ich jetzt den ln anwende
Falls man nicht gleich gesehen hat, dass die Lösungsmenge leer ist, sollte man es hier merken: Denn jetzt stünde auf der rechten Seite ln(0). Aber ln(0) ist nicht definiert. ---> die Lösungsmenge ist leer.
Vielen Dank für deine Hilfe - Ich muss dich dann noch einmal bitten dir die ganze Antwort anzusehen, da ich mit der Lösung nicht zum ergebnis komme.
Ich habe die Aufgabe als Antwort mit bild gepostet
Einen anderen Lösungsweg also der von Notizhelge ist dieser hier:
man kann einfach die Potenzgesetze anwenden:
e^(4) / e^(3) = e^(4-3)
Bei deiner Aufgabe:
e^(2-t+2) / e^(-1 + 0,5t ) = e^(-t) / e^(-1 + 0,5t)
Potenzgesetze:
= e^( -t +1 - 0,5t) = e^( -1,5t + 1) = 0
Jetzt kann man das auseinanderziehen:
e^(-1,5t) * e^1 = 0 Anweisung: teile durch e^1
e^(-1,5t) = 0
Die e-Funktion wird nie Null, damit gibt es keine Lösung.
Ja genau das hatte ich auch im Hinterkopf - wusste nur nicht mehr wie es nochmal genau ging...trotzdem habe ich keine ahnung wie ich auf die Lösung kommen soll.
Leider ist diese in einer sehr schlechten Qualität, sodass ich nur entziffern kann, dass die eben die beiden e geteilt haben und dann steht da e^(kann man nicht erkennen, müsste dann aber das sein, was wir berechnet haben)= 1
Ah jetzt sehe ich das, die haben nachdem die es geteilt haben e^(-1+1,5t)=1
Dann nehmen die den ln, sodass -1+1,5t=0 übrig bleibt und dann ist t=2/3
Doch frage ich mich wie kommen die auf das gleich 1?
Vielen Dank für deine Hilfe - Ich muss dich dann noch einmal bitten dir die ganze Antwort anzusehen, da ich mit der Lösung nicht zum ergebnis komme.
Ich übe grade fürs Abitur und habe alte Aufgaben durchgerechnet. Die Lösung bekommt für t0 =2/3 raus und ich hab dann absolut keine Ahnung wie ich von unserem erarbeitetem Ergebnis dahin kommen soll.


Meinst du den zweiten Teil von c)?
Der durchschnittliche Zuwachs in einem Zeitintervall entspräche dem Differenzenquotient. Der Momentanzuwachs zu einem bestimmten Zeitpunkt entspräche dem Differentialquotienten, also der Ableitung.
Ich würde die erste Ableitung bilden. Da die Bakterienzahl in Millionen angegeben ist, müsste man 100/1000000 = 1/100000 nehmen, dh den Zeitpunkt bestimmen, ab dem die erste Ableitung gleich 1/100000 ist. Allerdings komme ich da nicht auf 2/3.
ah nein ich mein den Aufgabenteil d)...hatte ich in der Bildunterschrift geschrieben - ist wohl untergegangen, tut mir leid
ah nein ich mein den Aufgabenteil d)...hatte ich in der Bildunterschrift geschrieben
Achja, das hatte ich übersehen. Ich schaue es mir später an, bitte etwas Geduld.
bei der c) komm 13,5 heraus - du hast eine 0 zu viel geschrieben 100/1000000=1/10000 und wenn man das gleich der Ableitung g'= 10*e^2-t setzt kommen dann die 13,5 raus...mhh da frage ich ich aber wie kommst du am Anfang an die 100/1000000? Also wenn da steht wann sind es weniger als 100Bakterien muss man das durch die 1Mio teilen, da verstehe ich den Sinn noch nicht hinter warum das so ist....
PS: Natürlich es eillt nicht, erstmal vielen vielen Dank, dass du dir überhaupt die Zeit für mich nimmst!
du hast eine 0 zu viel geschrieben
Stimmt.
da frage ich ich aber wie kommst du am Anfang an die 100/1000000?
Weil die Einheit auf der senkrechten Achse 1 Million ist. Man muss also die 100 Bakterien als Bruchteil von 1Million ausdrücken.
d)
Beide Ableitungen bilden (das hast du richtig gemacht) und dann die Gleichung
g´(t0 + 2) = h´(t0)
nach t0 auflösen. Wahrscheinlich hast du irgendwo falsch umgeformt. Jedenfalls müsste es heißen:
10e^(2 - (t0 + 2)) = 10e^(-1 + 0,5t0) |:10
e^(2 - (t0 + 2)) = e^(-1 + 0,5t0) | ln
2 - (t0 + 2) = -1 + 0,5t0
-t0 = -1 + 0,5t0
-1,5t0 = -1
t0 = 1/1,5 = 2/3
Bei deinem Bruch müsste es heißen " ...=1" statt "...=0". Man kommt so auch hin, ist aber etwas umständlicher.
Genial! Vielel vielen Dank, da war deine Methode schneller und leichter als die Musterlösung aus dem Abitur :D
ehm bei der Variante mit dem Bruch wie kamen die den da auf das =1? und nicht 0
ehm bei der Variante mit dem Bruch wie kamen die den da auf das =1?
a/a = 1
10e^(2 - (t0 + 2)) = 10e^(-1 + 0,5t0)
Beide Seiten durch 10e^(-1 + 0,5t0) ergibt:
10e^(2 - (t0 + 2)) / (10e^(-1 + 0,5t0)) = 1
stimmt hab daran gar nicht mehr gedacht...
mhh also muss ich dann 10*e(2-(t+2)) = 0 setzten und den Nenner vernachlässigen.
Wenn ich dann aber weiterrechner und t herausbekommen möchte dann wäre doch der nächste Schritt durch 10 teilen - bleibt nur nur das e hoch...
Wenn ich jetzt den ln anwende bleibt nur noch 2-(t+2)=0 und das wäre wiederum 2-t-2=0 also -t=0?
Ist das so richtig?