Division bei komplexen Zahlen?
Hallo liebe Community,
entweder berechne ich das hier völlig falsch, oder stelle die "Gleichung" falsch auf. Aber irgendwie komme ich oft nicht auf die Lösungen meines Profs. Ich habe hier mal ein Beispiel einer meiner Rechnungen und darunter seine Lösung eingefügt. Ein Rechenweg hat er uns leider nicht als Lösung gegeben. LG :)
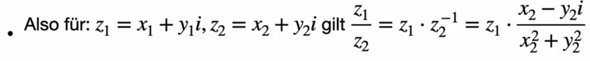
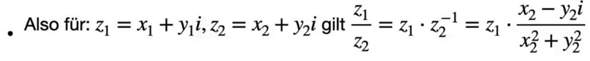
4 Antworten
Das ist mir schon in der zweiten Zeile zu wild. Wie kommt man denn auf sowas?
Ich kenne das so:
(-3 + 4i) / (5 + 7i)
Mit dem konjugiert komplexen Nenner erweitern:
((-3 + 4i)(5 - 7i)) / ((5 + 7i)(5 - 7i))
Ausmultiplizieren:
(-15 + 21i + 20i + 28) / (25 + 49)
Zusammenfassen:
(13 + 41i) / 74
Klammern vergessen!
Du hast eine Klammer vergessen. wie kommst du darauf die 4 der 4i des ersten Faktors zu kürzen? Oder die 2i danach mit dem Zähler des Bruches zu multiplizieren? Du mußt den ersten Faktor in Klammern setzen!
Ahh, die Klammer. Ich hatte das Konzept bei einem Kommilitonen gesehen und dann bei ähnlichen Typen angewendet. Es hat oft geklappt... :D
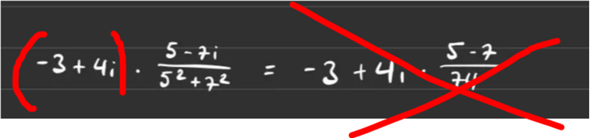
-3 * Bruch + 4i * Bruch
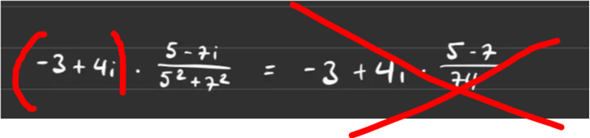
Vielen Dank, das sieht schon deutlich leichter aus! Unser Prof hatte uns da eine andere Gleichung angegeben, ich habe eigentlich nur eingesetzt