Aufleiten: z.B 2cos(2x) ... Wie leite ich das auf?
Danke, mit Begründung wäre ganz nett! :)
4 Antworten
Ich hoffe ich sag jetzt nichts falsches aber es müsste sin(2x) sein. Die aufleitung vom cosinus ist der positive Sinus. Da du ja die stammfunktion willst musst du dass in der Klammer mit dem forderten teilen. Also: 2/2
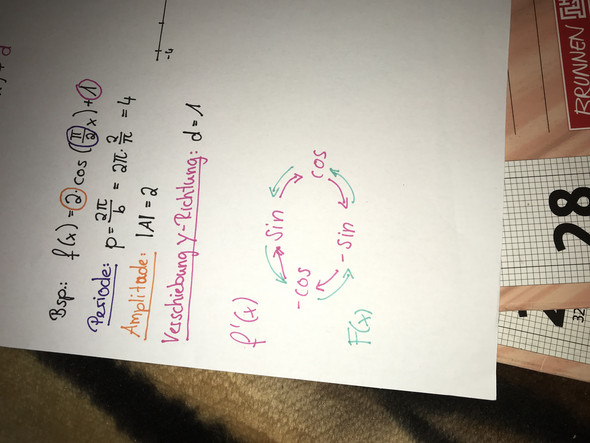
Leitest du jetzt das ganze wieder hab. Wird das in der Klammer mit vorne mal genommen also quasi 1x2 wäre dann 2cos(2x) in der Klammer bleibt alles gleich

Lass mich kurz überlegen. Eigentlich müsste es so sein: 2cos(2x) weißt du ja (siehe Bild) dass die erste Ableitung des positiven cosinus ein negativer Sinus ist. Willst du jetzt deine obige Funktion ableiten musst du also das in der Klammer (nur die Zahl) mit der davonstehlenden addieren also in dem Fall 2x2 dann hättest du folgende Ableitung von obiger Funktion: -4sin(2x) in der Klammer bleibt es also wieder gleich. Anders wie bei einer „Normalen“ bzw. Nicht Trigonometrischen Funktion verkleinert sich die Hochzahl da ja genau genommen keine vorhanden ist. Das 2x in der Klammer ist nicht mit dem x^2 zu vergleichen. Ich hoffe damit ist dir geholfen.
∫2*cos(2x) dx
t:= 2x
dt/dy = 2 <=> dt/2 = dx
∫2*cos(t) dt/2
∫ cos(t) dt = [ sin(t)+C] , C € IR
t:=2x
=> sin(2x) + C
Die Funktion kann man durch Substitution integrieren.
Es gilt
∫ 2cos(2x) dx = ∫ cos(u)du.
Jetzt musst du nur noch cos(u) integrieren und danach u resubstituieren.
siehe Mathe-Formelbuch "Integrationsregeln","Grundintegrale"
"Konstantenregel" Integral(a*f(x)*dx=a*Integral(f(x)*dx Konstanten können vor das Integralzeichen gezogen werden.
Integration durch "Substitution"
Integral(f(x)*dx=Integral (f(z)*dz*1/z´
F(x)=Integral(2*cos(2*x)*dx=2*Integral(cos(z)*dz*1/2
Substitution z=2*x abgeleitet z´=dz/dx=2 ergibt dx=dz/2
also F(x)= 2/2*Integral( cos(z)*dz
F(x)=sin(z) +C Rücksubstitution
F(x)=sin(2*x)+C
Hinweis: Die Integration durch die "Substitution" gelingt nur,wenn z´=dz/dx=konstant ist oder wenn sich das übriggebliebene "x" herauskürzt.
Beispiel: F(x)=Integral( x*(2+x^2)^2*dx
Substitution z=x^2+2 abgeleitet z=dz/dx=2*x ergibt dx=dz*1/(2*x)
F(x)=Integral(x*1/(2*x)*(z)^2*dz
F(x)=1/2*integral ( z^2*dz)=1/2*z^3*1/(3)
F(x)=1/6*z^3+C=1/6*(2+x^2)^3+C
Aber ich hätte noch eine Frage zum ABleiten, wenn jetzt die Hochzahl 2x ist, ist das dann genau gleich, wie wenn die Hochzahl xhoch2 ist?