Wie Löse ich die Aufgabe in Mathe?

Hey, wir schreiben am Montag eine Mathe Klausur und ich bin gerade am Üben. Nur habe ich eine Aufgabe wo ich einfach nicht weiter komme.
Wir haben die Funktion G(x)= 2•e^(-0,25x^2) die für das Intervall -2<x<2 die Unterkante eines gebogenen Abschlussbalkens einer Dachrundung ( Gaube). Dabei liegt die Gaube nicht direkt auf dem Dach sondern dazwischen ist noch ein 0,5m hoher Sockel (Rechteck).
In Gaube und Sockel soll nun ein rechteckiges Fenster rein, welches die Ränder der Glaube berühren darf. Wie hoch ist die Fensterfläche maximal?
mein Ansatz war das ich die Formel umändere in G(x)= 2•e^-0,25+ 0,5
und eine zweite Funktion A=a•b
aber was mache ich jetzt?
Vielen Dank für jede Hilfe😊🙏
2 Antworten
Wenn ich das richtig verstehe, wird das Fenster von der linken Intervallgrenze bei x=-2 bis zum Graphen gehen und in der Höhe von der x-Achse (von Deiner Funktion G) bis zum Graphen, oder?
Die Höhe des Fensters ist nun G_neu(x) [ich würde die Nebenbedingung nicht wie die Funktion in der Aufgabenstellung nennen!] und die Breite ist x+2 [von -2 bis x].
Das in A eingesetzt, ergibt A(x)=(x+2) * G_neu(x).
(in Deiner Frage hast Du das x vergessen, die Funktion lautet sicher G(x)=2e^(-0,25x))
Ja, x² macht mehr Sinn... Allerdings ist der Sockel 1m hoch, nicht 0,5!
Die Breite des Fensters ist dann 2x und die Höhe G_neu(x).
Also habe ich als Funktion A=g(x)•2x
was mache ich dann?
ja stimmt 0,5 ist dieses kleine lilane
A "heißt" A(x). Das ist nun die Funktion, die Dir für jedes x zwischen 0 und 2 sinnvolle Flächeninhalte liefert. Du musst nun das Maximum ausrechnen, d. h. A(x) ableiten, Null setzen, usw.
Also A(x) = g(x)•2x ableiten und Extrema berechnen aber ich bekomme da eine leere Menge raus
Ich habe nochmal ein Bild reingestellt, da kann man es besser erkennen
diese Fkt liefert ein Max

wie man sieht .
Wie ist denn die erste Ableitung ?
so
e^(-0.25 x^2) (4 - 2 x^2)................vergleiche sie mit deiner .
und man sieht , dass ( 4 - 2x² ) = 0 wird bei + und - wurzel(2).
du hast irgendwo einen Fehler in deinen Rechnungen .
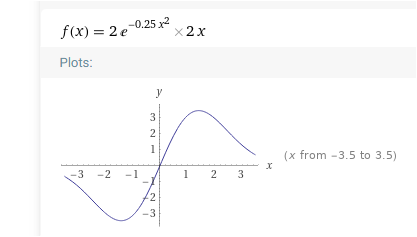
Das ist die Fläche ohne das Rechteck darunter. Rechnet man diese Fläche (=2x) hinzu, wird die Fläche immer größer, je weiter man nach rechts geht. D. h., die Fläche ist am größten, wenn sie am äußersten Rand der Gaube endet, also quasi fast komplett unter dem Geschwungenen liegt, was die Aufgabenstellung praktisch eigentlich unsinnig macht, kein Mensch würde das Fenster in einer Gaube so anordnen wollen... Es sei denn, es wurde hier etwas von der eigentlichen Aufgabenstellung weggelassen.
Ah ja genau x^2 kommt da noch dahinter