Wie kann ich den Brennpunkt einer Parabel bestimmen?

Moin, ich weiß prinzipiell wie man den Brennpunkt einer Parabel bestimmen und würde dazu eine Tangente nutzen, die die Steigung 1 hat bzw. 45°.

Mich interessiert aber wie ich den Brennpunkt bestimmen kann, wenn die Tangente nicht 45° hat, sondern eine beliebige. Als Beispiel habe ich mir überlegt, dass die Tangente den Punkt R(3|x) berührt. Auf dem Bild kann man das ganze vielleicht besser verstehen und meine bisherige Rechnung sehen:

Hab schon überlegt, dass man die Steigung der roten Tangente irgendwie durch den Schnittpunkt mit der schwarzen Tangente berechnen kann. Da bin ich aber nicht weiter gekommen. Eigentlich brauch ich nur den Ansatz wie ich die Steigung dieser Tangente berechne, bei dem Rest hab ich schon einen Plan.

Danke im voraus :)

Answer 1

[ProfFrink]

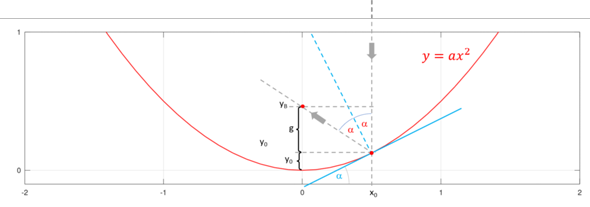
Das Bild zeigt eine allgemeine Parabel mit dem Scheitelpunkt (0 | 0). Der graue Pfeil markiert einen einfallenden Strahl an der Stelle x = x_0. Der Reflexionspunkt liegt im Punkt (x_0 | y_0) wobei der die Stelle y_0 einfach aus der Parabelformel gewonnen wird.

$y_0=a\cdot x_0^2$ Die Steigung der blauen Reflexionsebene entspricht der ersten Ableitung der Parabel an der Stelle x_0

$y'=2ax$ Die Steigung an der Stelle x_0 beträgt demnach

$\tan\alpha=2ax_0$ Der Winkel alpha wurde eingeführt weil nach dem Reflexionsgesetz gleich mit dem doppelten Winkel gerechnet werden muss.

Für das weitere Verständnis ist es wichtig zu sehen, dass sich der blaue Winkel alpha im roten Winkel alpha reproduziert. Der rote Winkel alpha spannt sich zwischen dem Einfallsstrahl und der Parabelsenkrechten am Reflexionspunkt auf. Nach dem Gesetz: Einfallswinkel gleich Ausfallswinkel ist hier nun der doppelte Winkel anzusetzen.

Für den Winkel 2*alpha wird wird nun die Gegenkathete und die Ankathete aufgesucht um eine passende Tangensformulierung aufzustellen. Es gilt

$\frac{x_0}{g}=\tan\left(2\alpha\right)$ bzw.

$g=\frac{x_0}{\tan\left(2\alpha\right)}$ Nun wird nach einem Additionstheorem der Tangens des doppelten Winkels durch einen Tangens des einfachen Winkels ersetzt.

$g=\frac{x_0\cdot\left(1-\tan^2\alpha\right)}{2\cdot\tan\alpha}$ wobei nun der Tangens von alpha durch die gefundene Steigung ersetzt werden kann.

$g=\frac{x_0\cdot\left(1-4a^2x_0^2\right)}{2\cdot2ax_0}=\frac{1-4a^2x_0^2}{4a}$ Zur Auffindung des Brennpunkts nach Zeichnung muss hier allerdings noch der offset von y_0 addiert werden.

$y_B=g+y_0=\frac{1-4a^2x_0^2}{4a}+ax_0^2=\frac{1-4a^2x_0^2}{4a}+\frac{4a^2x_0^2}{4a}$

Es bleibt

$y_B=\frac{1}{4a}$

Woher ich das weiß: Studium / Ausbildung

Comments

[sinareissmann]

Danke dir vielmals! Ich hab mir das zwar selbst am Beispiel irgendwie zusammen gewurschtelt und bin auf eine richtige Lösung gekommen, das allgemein zu sehen, hilft aber nochmal mehr!