Wie berechnet man die zurückgelegte Strecke der Draisinenfahrt (Integral)?

Aufgabe:

Die Abbildung zeigt den Geschwindigkeitsverlauf einer Draisinenfahrt für die ersten 60 Sekunden entlang eines geradlinigen Gleisabschnittes. Dieser Verlauf kann durch die folgende Funktion beschrieben werden.

v(t)= 1/3000t³ — 1/30t² + 4/5t   (0s < t < 60s)

a) Berechnen Sie den Weg, den die Draisine nach 30s zurückgelegt hat.

b) Ermitteln Sie den zurückgelegten Weg zwischen 15s und 30s.

c) Berechnen Sie den Weg, den die Draisine nach 60s insgesamt zurückgelegt hat.

Problem/Ansatz:

es geht hier um das Integral aber welche Formel muss ich hier benutzten?

Wie muss man das berechnen?

Ich bitte um Hilfe schreibe in fünf Tagen eine Klausur und verstehe es leider nicht. : /

Eine ausführliche Lösung mit erläutern zum nachvollziehen wäre an dieser Stelle sehr hilfreich. Ich Danke im Voraus!!

Answer 1

[RonaId]

Das Teil fährt ja irgendwann auch mal rückwärts. Und Einheiten vermisse ich auch. Aber was solls, dann ist das so.
Du bildest einfach das Integral, und das ist halt der Weg.

$=\dfrac{t^4}{12000}-\dfrac{t^3}{90}+\dfrac{2t^2}{5}$ Da kannst Du für t die Start-und Endzeiten einsetzen und entsprechend voneinander abziehen.

Bei 30 kommt glaub ich 127,5 wasauchimmer raus.

Bei 15 kommt dann 56,72 hin und wenn man das voneinander abzieht, dann wären das 70,78 wasauchimmer.

Woher ich das weiß: Berufserfahrung – Traktorist mit Zertifikat von Bill Gates

Answer 2

[Spikeman197]

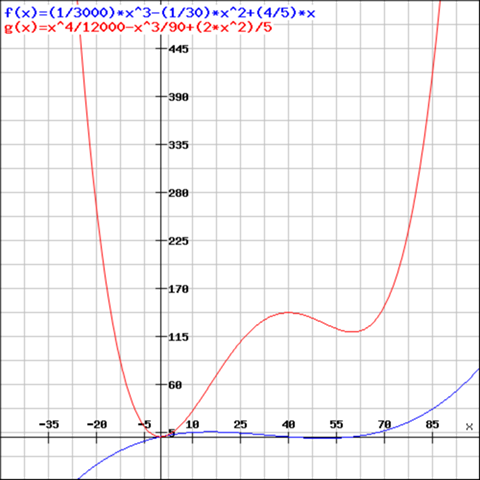
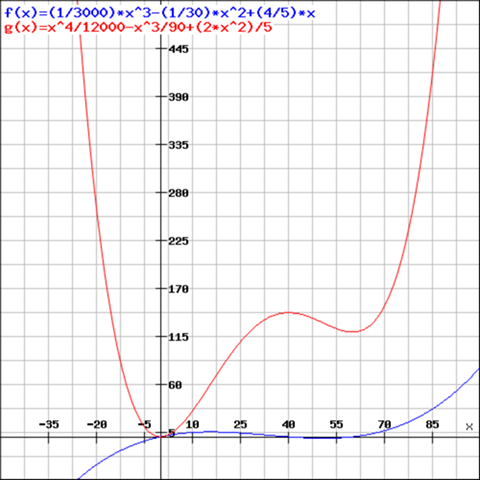
Das Integral der Geschwindigkeit über die Zeit ist die zurückgelegte Strecke.

Wenn v konstant ist, ergibt sich im Diagramm ein Rechteck (s=v×t). Steigt v in einer Ursprungsgeraden ist es ein Dreieck (s=1/2×v×t)

Hier hast Du eine kubische Funktion für v, also hoch 3, aber letztlich geht es nur um die Fläche unter dem Grafen.