Wie berechne ich die Regressionskoeffizienten einer multiplen Regression?
Es geht um eine multiple lineare Regression. Ich habe also eine abhängige Variable Y und mehrere unabhängige Variablen X1, X2, etc.
Dann habe ich verschiedene Regressionskoeffizienten: b0 ist der "Interzept", und dann jeweils b1, b2, etc. als Steigungen für die jeweiligen X-Variablen.
Ich finde nirgends die Formel zur berechnen von z.B. b2. Anscheinend ist die Formel anders als bei der bivariaten linearen Regression. Die wäre die, die ich im Bild hochgeladen habe.
Wenn ich diese Formel allerdings für b2 verwende, bekomme ich ein falsches Resultat. Ich habe natürlich alle X darin durch die Werte der X2 ersetzt. Außerdem ändert sich im Beispiel des Professor dann auch der Wert von b1 (wenn b2 dazu kommt). Ich weiß aber nicht, wie der Prof zu seinem Resultat kommt. Seine Rechnung ist auf jeden Fall richtig, denn Excel gibt das gleiche Resultat wieder.
Was mache ich falsch? Kann mir jemand helfen? Vielen, vielen Dank!
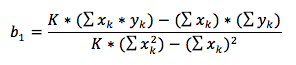
1) Ursprüngliche Tabelle:
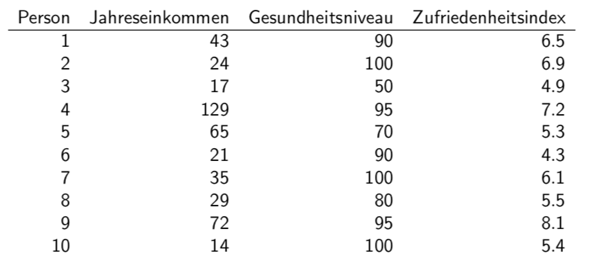
2) Berechnung für bivariate Regression (Jahreseinkommen + Zufriedenheit):

3) Berechnung der multiplen Regression (Jahreseinkommen + Zufriedenheit + Gesundheitsniveau):


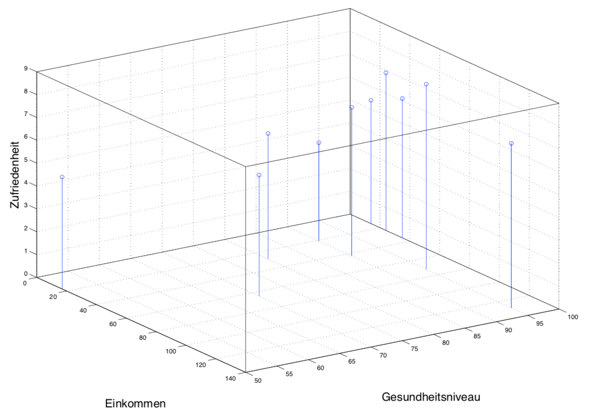
4) Darstellung in der Ebene
1 Antwort
Ich fürchte, dass da bei dir ein Verständnisproblem vorherrscht. Dein Professor macht keine lineare Regression für drei unabhängige Variable. Es sind nur zwei unabhängige Variablen, nämlich das Jahreseinkommen und das Gesundheitsniveau. Die vierte Spalte, also der Zufriedenheitsindex, ist das, was dein Modell vorhersagen soll, also dein y. In seiner Rechnung zeigt er ja auch explizit, wie die y-Werte geschätzt werden. Beachte, dass das b0 ein konstantes Glied ist, also ein Threshold. Dieser Term wird nicht verwendet, um eine der Variablen zu Gewichten, sondern gibt in dieser graphischen Darstellung eben nur an, wie "weit oben" die Ebene liegt, ab dem die Höhe der dargestellten Punkte gemessen wird.
Du kannst die Parameter b0, b1, b2 erhalten, indem du das Optimierungsproblem
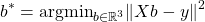
löst, wobei X eine Matrix ist, die für jede Zeile deiner Tabelle die beiden Werte für Jahreseinkommen und Gesundheitsniveau enthält. Außerdem wollen wir ja das konstante Glied berücksichtigen, d.h. wir fügen dieser Matrix noch eine Spalte hinzu, die nur Einsen enthält. Multipliziert man dann einen Spaltenvektor b mit drei Einträgen von rechts an die Matrix heran, wird der letzte Eintrag dieses Vektors einfach mit 1 multipliziert. Beachte, dass in dieser Darstellung der dritte Eintrag des Vektors b gerade dem b0, also dem Threshold von oben entspricht. Der Vektor y hat gerade so viele Einträge wie es Zeilen in deiner Tabelle gibt und jeder Eintrag entspricht dem Zufriedenheitsindex der jeweiligen Instanz.
Man mag sich fragen, wie man nun aus der Zielfunktion das optimale b herausbekommt. Naja, die Theorie konvexer Optimierungsprobleme legt nahe, dass wir den Gradienten bestimmen und dann schauen müssen, für welches b dieser verschwindet. Wenn ich das tu, erhalte ich die Bedingung
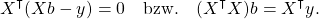
Aber die Gleichung auf der rechten Seite entspricht einfach nur einem linearen Gleichungssystem. Und das können wir lösen! Da wir im 21. Jahrhundert leben, machen wir das aber nicht per Hand, sondern nutzen eine der zahlreichen Bibliotheken oder Programme, die unser Werkzeugkasten so hergibt. Wenn du das per Excel machen willst, ist das vollkommen in Ordnung. Du musst auch gar nicht den Weg gehen, erst dieses lineare Gleichungssystem aufzustellen - das machen die Programme intern natürlich automatisch, wenn du einfach eine Funktion wie linear_regression() nutzt und dann deine Werte einsetzt.
Ich habe das Ganze aber mal in Python implementiert, um dir zu zeigen, dass das auch tatsächlich funktioniert. Der Code ist recht überschaubar:
import pandas as pd
import numpy as np
def linear_regression(data):
data = data.to_numpy()
X, y = data[:, :-1], data[:, -1]
X = np.concatenate((X, np.ones((X.shape[0], 1))), axis=1)
b = np.linalg.solve(np.matmul(X.T, X), np.dot(X.T, y))
return b
if __name__ == '__main__':
cols = {'einkommen' : [43, 24, 17, 129, 65, 21, 35, 29, 72, 14],
'gniveau': [90, 100, 50, 95, 70, 90, 100, 80, 95, 100],
'zufriedenheit': [6.5, 6.9, 4.9, 7.2, 5.3, 4.3, 6.1, 5.5, 8.1, 5.4]}
df = pd.DataFrame(cols)
b = linear_regression(df)
print(b)
Die Ausgabe lautet
[0.01740046 0.02964865 2.65928629]
Und wenn man jetzt berücksichtigt, dass der dritte Eintrag in b eben deinem b0 von oben entspricht, scheint das Ergebnis auch präzise mit dem übereinzustimmen, was dein Professor angegeben hat.
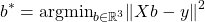
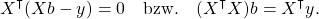
so ist es richtig , ich vermute aber , der FS möchte eine Formel so wie oben die "Schulformel" für b1 .