Wahrscheinlichkeiten berechnen Aufgabe?
Kann mir bitte wer helfen? Die Aufgabe lautet: Unter 100 Losen sind 20 Gewinne. Der erste Käufer erwirbt 5 Lose. Wie groß ist die Wahrscheinlichkeit dafür, dass darunter ein Gewinnlos ist?
5 Antworten
Die Wahrscheinlichkeit, dass darunter genau ein Gewinnlos ist:
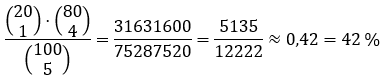
[Es gibt insgesamt binomial(100, 5) Möglichkeiten 5 Lose aus den 100 Losen auszuwählen. Dabei gibt es binomial(20, 1)*binomial(80, 4) Möglichkeiten 1 Los aus den 20 Gewinnerlosen und die anderen 5 - 1 = 4 Lose aus den 100 - 20 = 80 anderen Losen zu ziehen.]
===========
Die Wahrscheinlichkeit, dass darunter mindestens ein Gewinnlos ist:
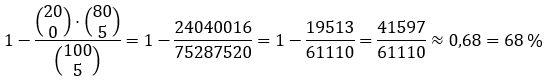
[Idee: 1 - Gegenwahrscheinlichkeit, dass kein Gewinnlos]
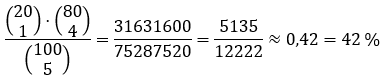
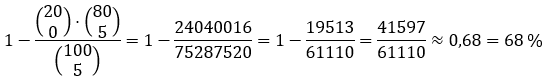
Nein, zwischen der 20 und der 1 ist kein Bruchstrich, es handelt sich um einen Binomialkoeffizienten binomial(20, 1). Gesprochen: „20 über 1“ oder „1 aus 20“
Hallo,
soll unter den fünf Losen genau ein Gewinnlos sein, also ein Gewinn und vier Nieten?
Dann rechnest Du mit Binomialkoeffizienten n über k:
[(20 über 1)*(80 über 4)]/(100 über 5)=0,42 oder 42 %.
Unter den fünf gekauften Losen soll eins aus der Gruppe der 20 Gewinnlose stammen, vier aus der Gruppe der 80 Nieten.
Insgesamt werden fünf aus hundert Losen gezogen.
Den Binomialkoeffizienten findest Du auf dem Rechner unter der nCr-Taste.
4 über 1=4 nCr 1=4 usw.
Herzliche Grüße,
Willy
Ist es mindestens eins, ziehst Du die Gegenwahrscheinlichkeit, nämlich fünf Nieten, von 1 ab:
1-[(20 über 0)*(80 über 5)]/(100 über 5)=68,1%
evtl. ist dieser Fall für den Fragesteller einfacher als Produkt entlang des Pfades zu bestimmen (falls ihn die Formel der hyp. Verteilung umhaut)
wenn es genau ein Gewinnlos sein soll, ist die Wahrscheinlichkeit 5 über 1 mal 0,2 hoch 1 mal 0,8 hoch 4.
Wenn es mindestens ein Gewinnlos sein soll, ist die Wahrscheinlichkeit die Summe der Einzelwahrscheinlichkeiten für die Fälle 1 Gewinn sowie 2, 3, 4 und 5 Gewinne. Diese Einzalwahrscheinlichkeiten errechnen sich nach demselben Schema für eine Binomialverteilung, bei 3 Gewinnen also 5 über 3 mal 0,2 hoch 3 mal 0,8 hoch 2.
Das Ganze kriegst du einfacher mit dem Rechner raus, im ersten Fall mit
binompdf (5; 0,2; 1) wenn der Rechner die übliche Reihenfolge n,p,k bei der binomialverteilung hat.
im zweiten Fall:
1 - binompdf (5; 0,2; 0), also über die Gegenwahrscheinlichkeit.
Die Wahrscheinlichkeit, dass kein Gewinnlos
darunter ist, ist
80/100 * 79/99 * 78/98 * 77/97 * 76/96 = 0.32
Also ist die Wahrscheinlichkeit für mindestens
ein Gewinnlos 0.68.
wie genau bist du auf deine rechnung gekommen? danke im vorraus
swchreib mal bitte deinen ganzen lösungsweg
Man macht das über die Gegenwahrscheinlichkeit.
Vorausgesetzt, du wolltest wissen, mit welcher
Wahrscheinlichkeit mindestens ein Gewinnloa
dabei ist und nicht genau eins.
Das Gegenteil von "mindestens 1" ist "keins".
Wir rechnen also aus, wie wahrscheinlich es
ist, kein Gewinnlos zu ziehen und ziehen diese
Wahrscheinlichkeit von 1 ab.
Beim ersten Ziehen ist die Wahrschinlichkeit
für eine Niete 80/100. Beim zweiten Mal ist sie
79/99, denn es ist eine Niete raus und ein Los,
usw. Alle Wahrscheilichkeiten werden multipliziert,
denn du willst ja beim ersten Mal eine Niete haben
und beim zweiten Mal usw.
Das ergibt eine Wahrscheinlichkeit von 0.32,
die für mindestens ein Gewinnlos ist also
1-0.32 = 0.68.
oke jetzt habe ich das verstanden. Vielen dank für deine mühe"
Oben stehen die "günstigen", unterm Bruchstrich die möglichen, das ergibt die Einzelw.keit für einen Zug:
80 (kein Gewinnlos) durch 100 (alle Lose)
nächster Zug 79/99 (ein los weniger)
usw.
und Produkt daraus bilden. Von eins abziehen, da Gegenereignis gesucht ist.
Hab ich geschrieben, während der andere Kommentar verfasst wurde...
Hinweis: Hypergeometrische Verteilung.
_
Vielen danke! Das ist so unglaublich gut erklärt DANKE<3!!!!!!