Vollständige Induktion, Term erweitern erlaubt?

Liebe GuteFrage - Community,

ich übe mich derzeit an Beweisen und habe mich vorhin gefragt, ob diese Lösung für den folgenden Beweis korrekt ist. Ich habe den Term ja mit 3 multipliziert und frage mich, ob das innerhalb einer vollständigen Induktion überhaupt erlaubt ist. Das fühlt sich nämlich eher falsch an. LG, Manu

Answer 1

[Willy1729]

Hallo,

wieso machst Du es Dir so kompliziert?

Bei der vollständigen Induktion darfst Du (nachdem der Induktionsanfang gezeigt ist) die Induktionsvoraussetzung benutzen.

Du nimmst als wahr an, daß n³+(n+1)³+(n+2)³ durch 9 teilbar ist und zeigst, daß die Behauptung dann auch für n+1 stimmt.

Für n+1 lautet der Term (n+1)³+(n+2)³+(n+3)³.

Ziehst Du davon n³+(n+1)³+(n+2)³, einen laut Voraussetzung durch 9 teilbaren Term ab, muß ein durch 9 teilbarer Term übrigbleiben, falls die Behauptung stimmt.

Da (n+1)³+(n+2)³ sofort abgezogen werden können, ohne erst ausmultipliziert werden zu müssen, bleibt (n+3)³, von dem n³ abgezogen wird, denn mehr ist von der Voraussetzung nicht übriggeblieben.

Das ergibt 9n²+27n+27=9*(n²+3n+3), ein zweifelsohne durch 9 teilbarer Term.

Das war's dann auch schon.

Herzliche Grüße,

Willy

Comments

[Willy1729]

Vielen Dank für den Stern.

Willy

[manu2608]

Genau diese Methode sah ich auch bei Herrn Professor Weitz auf YouTube und wurde dadurch etwas "kreativer". Aber erst jetzt verstehe ich das Prinzip dahinter! Vielen Dank für die tolle Erklärung!

Answer 2

[evtldocha]

Ich habe den Term ja mit 3 multipliziert

... zumindest induzierst Du damit eine eventuell nicht vorhandene Teilbarkeit durch 3 und das sollte Dir dann auch sagen, dass das so nicht geht.

Nachtrag:

Ich würde das durch eine Umformulierung der Induktionsvoraussetzung lösen:

$IV:\ \exists\ n\in\mathbb{N}:\ n^3+\left(n+1\right)^3+\left(n+2\right)^3\ |\ 9\ \ \$ $\Rightarrow\ \exists\ k\ \in\mathbb{N}:\ 9\cdot k\ =\ n^3+\left(n+1\right)^3+\left(n+2\right)^3$ $\Rightarrow\ \left(n+1\right)^3+\left(n+2\right)^3=9\cdot k\ -\ n^3$

Damit kann man den Induktionsschritt so schreiben:

$IS:\ \ n\ \to n+1$ $\left(n+1\right)^3+\left(n+2\right)^3+\left(n+3\right)^3=^{\left(IV\right)}9\cdot k-n^3+\left(n+3\right)^3=$ $9⋅k−n^3+n^3+3⋅n^2⋅3+3⋅n⋅3^2+3^3\ =\ 9\cdot\left(k+n^2+3n+3\right)$ Das hat also den Faktor 9 und ist damit durch 9 teilbar.
■

Comments

[manu2608]

Ich habe es mir schon fast gedacht, es wäre auch zu einfach gewesen... :D

[evtldocha]

@manu2608

Das sind ja keine Gleichungen, mit denen man Äquivalenzumformungen machen kann, sondern Terme, die so lange umgeformt werden müssen, bis das Gewünschte da steht.

[Willy1729]

@evtldocha

So könnte man auch beweisen, daß n+8 durch 9 teilbar ist:

Induktionsanfang für n=1:

1+8=9 und 9 ist durch 9 teilbar.

Erweitern mit 9:

9*(n+8)=9k und 9k ist durch 9 teilbar.

Answer 3

[Halbrecht]

gutes Gefühl . Denn was man rechts vom = macht , soll auch links vom = geschehen

.

Kenn mich mit Beweisen nicht aus

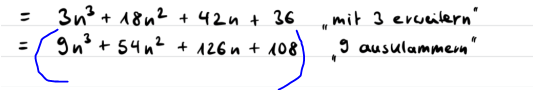
/3 kann man machen . Was es bringt weiß ich nicht

Comments

[manu2608]

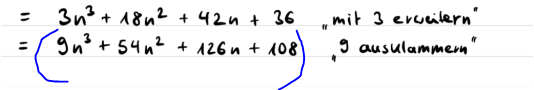
Ahhh okay, das Teilen ist also erlaubt und gilt dann als Äquivalenzumformung?

[Halbrecht]

@manu2608

nicht teilen

wenn man die Terme mit MAL 3 behandelt , muss man als Ausgleich eben DURCH 3 mit einführen

Ist wie mit der nahrhaften Null bei der quadratischen Ergänzung

aus x² + 4x + 7 wird ( (x+2)² - 4 + 7 ) .............-4 weil man 2² dazu"gezaubert" hat.

[manu2608]

@Halbrecht

Ich verstehe, nur hat man dann in meinem Fall natürlich nichts damit gewonnen :D