Handelt es sich hierbei um die Bernoulli Ungleichung?
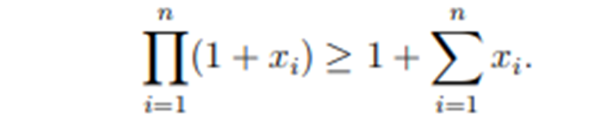
Oder ist es doch eine Abwandlung. Wenn nicht wie könnte man sie dann mit vollständiger Induktion beweisen. Ansatz wäre auch gut
2 Antworten
Ich habe die Vermutung für den Fall dass alle x_i größer gleich 0 sind bewiesen.
Für den Fall dass die x negative Werte annehmen, habe ich ein Gegenbeispiel gefunden.
n=2 x1=-1 x2=1 0>1
Für mich sieht das nicht nach Bernoulli aus.
Beweisskizze liegt bei. Da ich kein Mathematiker bin, dürfte einiges formal nicht zufriedenstellend sein.


Das ist ein Mal. Du hast die für irgendein n bestätigte Vermutung und multiplizierst mit (1+x_n+1) um die linke Seite für n+1 zu haben.
Der Beweis sollte ähnlich wie der von der Bernoulli Ungleichung ablaufen.
Schau dir also den Beweis davon an und Versuche die argumente hierauf anzuwenden.
(Du musst aber beachten, dass die Ungleichung im allgemeinen nur gilt, wenn alle xi größer als -1 sind und alle das selbe Vorzeichen haben)
Vielen Dank. Ich hätte noch zwei kleine Fragen. In der zweiten Zeile wo hinter dem I steht (1+xi) was steht da zwischen dem (1+Exi) und dem (1+xn+1), ist das ein mal oder ein plus