Verändert sich der Grad einer Parabel wenn sie 3D wird?
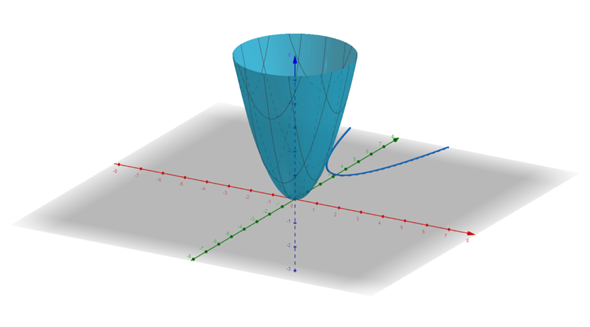
In dem Bild ist es einmal dargestellt. Verändert sich der Grad der Funktion wenn die Parabel zu solch einen 3D-Trichter wird?
PS: Ja, ich habe absolut keine Ahnung von Mathe.
3 Antworten
Auf dem Bild zu sehen ist: z= x^2 + y^2 .
Der Grad der algebraischen Funktion ist hier zweiter Ordnung <=> Quadratisch <=> Parabel.
Das bleibt auch so in beliebig vielen Dimensionen:
z = sum of (x_i ^2) from i=1 to oo
Das 3-dimensionale Ding heißt Drehparaboloid (oder Rotationsparaboloid); es entsteht durch Drehung (=Rotation) um die Symmetrieachse der Parabel - der Grad ändert sich dadurch nicht unbedingt (allerdings bin ich mir nicht sicher, ob man bei 3-dimensionalen Gebilden auch von 2., 3. 4. ... Grad spricht)
Das Bild stammt aus GeoGebra; das Paraboloid hat (vermutlich) die gleichung f(x,y)=x²+y².
Du kannst - wenn du das selbst in GeoGebra gemacht hast - ja mal der Reihe nach eingeben
- f(x, y)=x²+y⁴
- f(x, y)=x⁴+y⁴
- f(x, y)=x⁴+y²
und sehen, was passiert 😊
Der Grad einer Abbildung\Funktion ist bestimmt durch die höhste Ordnung. Dadurch sind deine drei Beispiele alle nicht quadratischer sondern quartischer Ordnung bzw. Grad.
Was meinst du mit Grad, Parabeln sind immer zweiten Grades
Ja genau das. Ich wusste nur nicht ob sich das ändert, wenn es diese dreidimensionale Form annimmt :D