Umlaufzeit/Periodendauer mit Masse und Radius bestimmen?
Hallo!
Die Aufgabe lautet:
Der Mond der Erde hat eine mittlere Entfernung von 384400 km. Wir groß ist die Umlaufzeit des Mondes um die Erde (Erdmasse M = 5,97410^24 kg)?
Welche Formel muss ich hier benutzen? Danke!
3 Antworten
Hier muss man davon ausgehen, dass die Mondbahn kreisförmig ist. Da der Mond sich kaum von der Erde wegbewegt, kann man die Radialkraft des Mondes mit seiner Gravitationskraft in Bezug zur Erde gleichsetzen. Mit der Geschwindigkeit in der Radialkraft und dem Umfang der Kreisbahn kann man dann die Umlaufzeit ausrechnen.
Das 3. Keplersche Gesetz nützt hier übrigens nichts.
U die Umlaufzeit,
a die Große Halbachse, (Große Halbachse des Mondes: 384.400 Kilometer)
M1 und M2 die Massen des Zentralkörpers und des Satelliten, (M1 Erde, M2 Mond)
G die Gravitationskonstante.
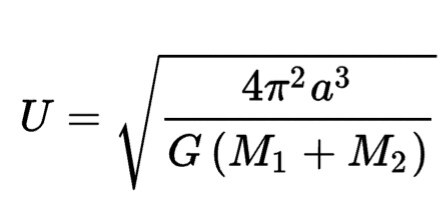
Kepler III google das mal ... ich weiß die formel nicht mehr genau