Steckbriefaufgabe Funktion 5. Grades gesucht?
Die Bedingungen sind, dass der Graph 5. Grades punktsymmetrisch sein muss, dort die Steigung 4 hat und bei x = 1 und x = 2 lokale Extremstellen. Deshalb sind meine Ansätze:
f(x) = ax⁵ + cx³ + ex
f'(x) = 5ax⁴ + 3cx² + e
f'(0) = 4
f'(1) = 0
f'(2) = 0
Wenn ich das in den Taschenrechner eingebe (wir haben es ohne Taschenrechner noch nicht gelernt), ist das Ergebnis falsch und ich weiß nicht warum
Ups hatte mich vertippt gehabt, die Funktion lautet f(x) = 1/5x⁵ - 5/3x³ + 4x
1 Antwort
Ansätze vollkommen korrekt .
Tut mir leid, das zu sagen : Nicht wirklich schwierig :))
.
Mit deinen Angaben sollte
4 = e ;
0 = 5a + 3c + 4 ;
0 = 80a + 12c + 4
.
Freund Wolfram sagt dann
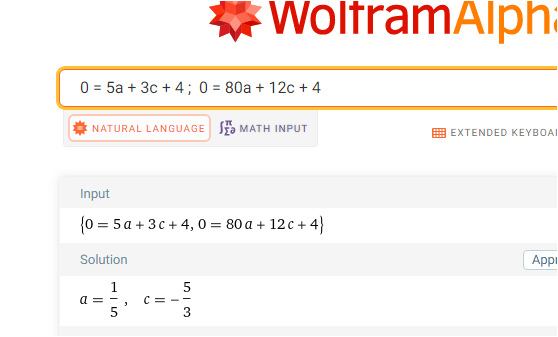
PS : ohne TR müsste man das tun
0 = 5a + 3c + 4 ; ....................diese Glt mal -16 und zur anderen addieren
0 = 80a + 12c + 4
0 = -80a - 48c - 64
-----------------------------
0 = 0 - 36 c - 60
60/-36 = c = -10/6 = -5/3
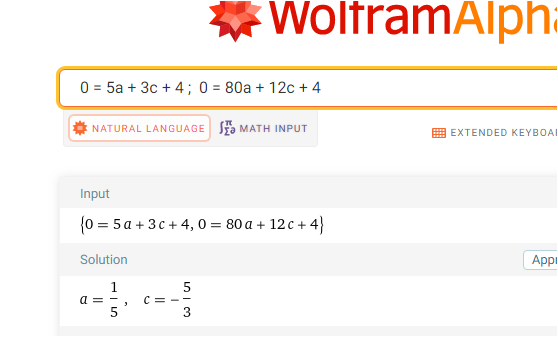
Jap, hab das auch rausbekommen. Glaub ich hatte mich vertippt, weshalb es zu Fehlern kam