Sinus / Cosinus ohne Taschenrechner berechnen?
Gibt es eine Formel, mit der man herausfinden kann, wie hoch die Sinus/Cosinus-Funktion für ein bestimmten Wert ist. Also, z.B. dass cos(π/3)=1/2
5 Antworten
Läuft dann auf die Betrachtung spezieller Dreiecke (rechtwinklig oder gleichseitig) hinaus.
Ja, es gibt Formeln (Reihenentwicklung), aber auch die sind ohne Taschenrechner zumindest mühsam.
Bei so speziellen Winkeln wie pi/3 = 60° kann man sich die Längen mit Pythagoras berechnen.
Ja, für einige spezielle Winkel (z.B. für den von dir genannten) geht das mit dem Satz des Pythagoras.
Es gibt ein paar leicht zu merkende:
- sin 30° = 1/2*sqrt 1
- sin 45° = 1/2*sqrt 2
- sin 60° = 1/2*sqrt 3,
- sin 90° = 1/2*sqrt 4
Ja sinus und kosinus kann man so als Reihen definieren
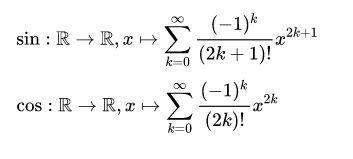

ja. es macht nur keinen spaß und man bekommt nur Näherungslösungen raus weil du keine unendliche reihe entwickeln kannst
Der taschenrechner rechnet auch nicht bis unendlich aber wenn er bis n=25 statt unendlich rechnet schickt das
sicher.. es reichen auch schon 3 oder 4 Glieder bei Reihenentwicklungen um für 90% der Sachen genau genug zu sein aber rein technisch gesehen weinen die Mathematiker weils eben nur Näherungen sind.
Mathematiker selber sind heuchler und machen vieles mit näherungen weil sie keine besseren verfahren haben manchmal
Und das kann man per hand rechnen