Polynom mit einer vorgegebenen Nullstelle?
Hallo,
f hat den Grad 3 und besitzt genau eine Nullstelle x = 2.
Wie ist der Ansatz, um f(x) zu finden?
Danke schonmal
3 Antworten
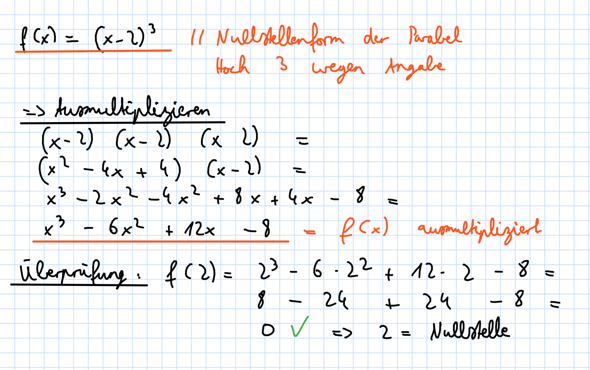
Da du die Angabe der Nullstelle hast und des Grades der Funktion, kannst du die Nullstelle einfach in die Nullstellenform einsetzen mit Grad 3 (Plus wird zu Minus, Minus zu Plus bei der Nullstellenform).

Eine Nullstelle bei x = 2 und Grad drei.
Heißt: Die Funktion faktorisiert sich folgendermaßen...
PS: Ich bin jetzt davon ausgegangen, dass "genau" eine Nullstelle heißt, dass es keine anderen gibt. Aber evtl. zählen dreifache Nullstellen nicht. Wenn dem so sein sollte, halte dich an gebrochen2 oder finde eine andere Funktion, die f(x) = (x-2)*z mit z als quadratischer Term, der nur komplex lösbar ist.
Also eine Nullstelle bei x = 2 gibt den Linearfaktor (x-2), denn wenn du dir x die 2 einsetzt, ist die Klammer null.
Da der dritte Grad gefordert ist, brauchst du noch „zwei x mehr“. Diese Linearfaktoren dürfen keine Nullstelle über den reellen Zahlen haben, also sowas wie (x^2 +1).
Also dann: f(x)=(x-2)*(x^2+1)
Denn wenn eine der Klammern null ist, ist alles null und es kann nur die linke Klammer null werden, die rechte wird nie null.