Minimaler Grad bei ganzrationalen Funktionen?
Hallo =), ich bin gerade am lerne und verstehe diese Aufgabe nicht ganz
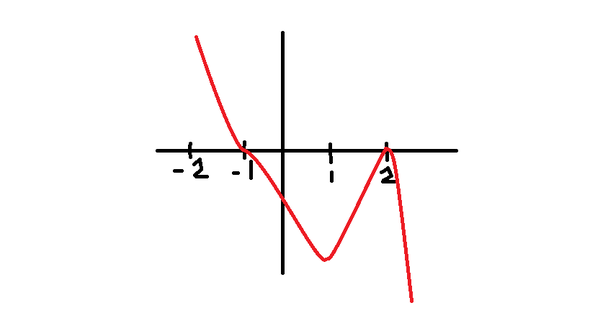
1.0 Der Graph in der Abbildung gehört zu einer ganzrationalen Funktion f mit minimalem Grad.
1.1 Begründen sie welchen Grad die Funktion f besitzt
Die vorgegebene Antwort lautet: Da die Funktion f minimalen Grad hat und eine doppelte und dreifache Nullstelle besitzt, muss der Grad der Funktion fünf sein.
(Siehe Bild Anhang)
Meine Frage ist was ist der minimale Grad und woran erkenne ich das hier eine dreifache Nullstelle vorliegt ich kann das ja schlecht einfach mal raten also muss dieser minimale Grad etwas damit zu tun haben.
Entschuldigt meine miese Zeichnung ;) Danke schonmal =).
1 Antwort
Also dass es eine dreifache Nullstelle gibt, erkennt man an diesem Bild schon mal gar nicht :D
Guck dir mal die Graphen der Funktionen f(x)=x, f(x)=x², f(x)=x³ an. Dann siehst du, was einfach, zweifache, dreifache Nullstellen sind.
Naja und die Vielfachheiten der Nullstellen geben halt dann an, wie hoch der Grad mindestens sein muss und da die Funktion nach Angabe minimalen Grad besitzt, ist sie eben von Grad 5.
Was ist der minimale Grad?
Der Grad ist ja der höchste Exponent vom x, wo der Koeffizient nicht 0 ist. Wenn eine Funktion eine Nullstelle hat, hat sie mindestens Grad 1 (sonst wäre es ja eine konstante Funktion). Wenn sie eine doppelte Nullstelle hat, hat sie mindestens Grad 2. Wenn sie eine dreifache Nullstelle hat, hat sie mindestens Grad 3. Wenn sie (wie oben) eine zweifache und eine dreifache Nullstelle hat, hat sie mindestens Grad 2+3=5.
Der Lehrer gibt dir nun vor, dass sie den MINIMALEN GRAD haben soll. Dann weißt du, dass es Grad 5 sein muss. Ohne diese Angabe könnte es auch Grad 6, 13 oder 475 sein.
Kann ich hier dreifache Nullstelle einfach so ablesen?
Wie ich oben schon geschrieben habe, aus deiner Krakelzeichnung kannst du den absolut nicht rauslesen. Aber da es bei dir Aufgabe wohl nur um qualitativen Verlauf den daraus resultierenden Folgen für den Grad der Funktion geht, wirst du den wohl aus dem Graphen "lesen" dürfen, wenn eine terassenpunktähnlich aussehende Nullstelle eingezeichnet ist.
Comprende?
Ich verstehe es immer noch nicht. Was ist der minimale Grad? Das mit den Exponenten weiß ich. Kann ich hier dreifache Nullstelle einfach so ablesen? Ich meine ich weiß wie eine aussieht aber was hat das mit dem* minimalen Grad* zu tun (ich hänge echt an diesem Wort)