Mathe Textaufgabe mit e-Funktion?
Hallo,
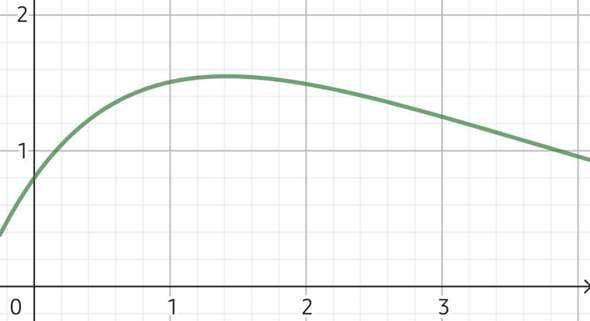
Die Aufgabe seht ihr hier. Ich komme überhaupt nicht zurecht mit den Aufgaben. Bei a) hab ich einfach den höchsten y-Wert der gegeben Funktion aufgeschrieben und dass ungefähr zwischen 0,16 und 3,86 h die Änderungsrate der Füllhöhe bei über 1 m/h beträgt, da bin ich mir aber nicht sicher. Bei b) verstehe ich nichts mehr

1 Antwort
Hallo Gamergg,
Bei a) hab ich einfach den höchsten y-Wert der gegeben Funktion aufgeschrieben ...
woher weißt Du genau, was der höchste Wert von
(1) h(t) = 4∙exp(−0,15∙t) − 2∙exp(−t) − 1,2
ist? Darfst Du GeoGebra o.ä. benutzen? Falls nicht:
Um wirklich sicher zu sein, musst Du eigentlich das t finden, wo h(t) maximal wird. Dazu muss zunächst
(2.1) h'(t) = −0,6∙exp(−0,15∙t) + 2∙exp(−t) = 0
sein, vorher positiv und nachher negativ sein. Wenn das so ist, musst Du diesen t- Wert in h(t) einsetzen. Zunächst ist
(2.2) 2∙exp(−t) = 0,6∙exp(−0,15∙t);
wir trennen die Exponentialteile von den Vorfaktoren:
(2.3) 0,3 = exp(−t)/exp(−0,15∙t) = exp(−0,85∙t)
Dann logarithmieren wir beide Seiten und teilen schließlich durch den Vorfaktor:
(2.4) t = ln(0,3)/−0,85 ≈ 1,464.
Vorher überwiegt in der Tat der positive Term, nachher der negative. Setzt man dies in h(t) ein, erhält man ca. 1,549.
... und dass ungefähr zwischen 0,16 und 3,86 h die Änderungsrate der Füllhöhe bei über 1 m/h beträgt, ...
Kommt ungefähr hin:
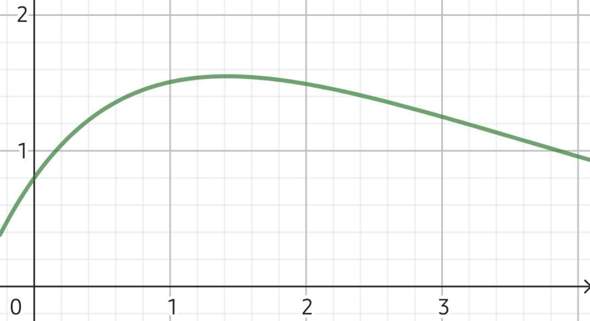
Abb. 1: Die Funktion h(t)
Allerdings wollen die Leute wahrscheinlich die Uhrzeit wissen. Und dies ist dann etwa zwischen 08:10 Uhr (eine Sechstelstunde nach Beginn) und kurz vor 12:00 Uhr.
Bei b) verstehe ich nichts mehr.
Dazu brauchst Du die Stammfunktion
(3.1) H(t) = −26⅔∙exp(−0,15∙t) + 2∙exp(−t) − 1,2∙t + C
von h(t). C muss so gewählt werden, dass H(0) = 1,5 ist. Da exp(0) = 1 ist, ist C = 26⅙ und daher
(3.2) H(t) = −26⅔∙exp(−0,15∙t) + 2∙exp(−t) − 1,2∙t + 26⅙.
Um herauszufinden, wie hoch der Stand um 13:00 Uhr ist, müssen wir t=5 einsetzen.