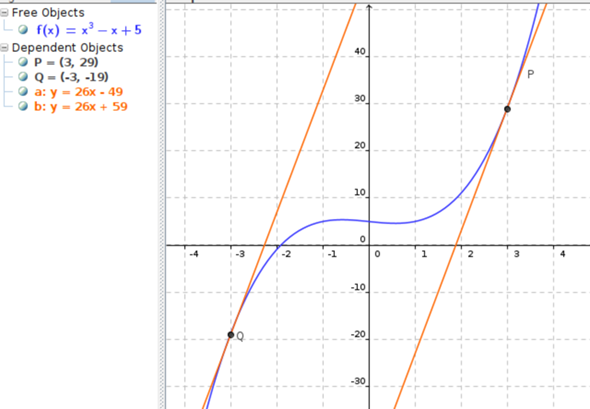
Mann sollte einen von P verschiedenen punkt Q auf dem graphen der Funktion f bestimmen , in dem die Tangente parallel zur Tangente im Punkt P ist.?
Mann sollte einen von P verschiedenen punkt Q auf dem graphen der Funktion f bestimmen , in dem die Tangente parallel zur Tangente im Punkt P ist.
f(x) = x^3-x+5 P(3/f(3))
wie berechne ich das?
1 Antwort
Hallo,
keine Ahnung, ob dir eine Antwort jetzt noch hilft.
Zur Aufgabe:
Die Steigung der Tangente an Graph(f) im Punkt P(3|f(3)) beträgt f'(3).
Man sucht also eine reelle Zahl a ≠ 3 für die gilt: f'(a) = f'(3) .
Um a zu finden, bilden wir zunächst die Ableitung von f :
f'(x) = 3x² - 1
Es gilt f'(3) = 3•3² - 1 = 26
Wie man sieht, gilt auch f'(-3) = 3•(-3)² - 1 = 3•3² - 1 = 26 = f'(3)
Das bedeutet: im Punkt Q(-3|f(-3)) beträgt die Steigung der Tangente an Graph(f) ebenfalls 26.
Berechnen wir die y-Koordinate von Q:
f(-3) = (-3)³ - (-3) + 5 = -27 + 3 + 5 = -19 , d.h. Q hat die Koordinaten (-3|-19).
Im Punkt Q(-3|-19) ist die Tangente an Graph(f) parallel zur Tangente in P(3|f(3)).
Anbei noch eine Grafik (x- und y-Achse mit verschiedenem Maßstab), die Graph(f) und die zwei parallelen Tangenten zeigt:
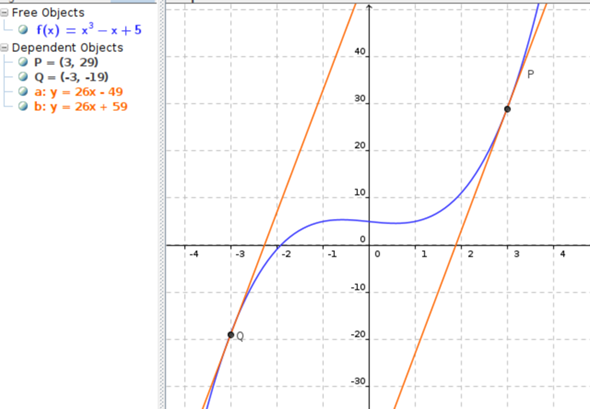
Gruß