Mathe? Extrempunkte? Kurvendiskussion?
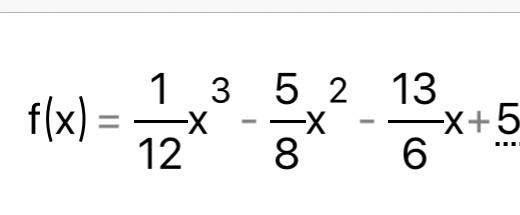
Aufgaben zur Funktion im Bild
d) Berechnen Sie die Schnittpunkte des Graphen von f mit den Koordinatenachsen.
f) Berechnen Sie die Koordinaten der lokalen Extrempunkte.
g) Berechnen Sie die Koordinaten der Wendepunkte.
h) Berechnen Sie die Gleichung der Tangente an den Graphen von f im Punkt P(1| yp).
i)Berechnen Sie alle Schnittpunkte des Graphen von f mit der Tangente aus Teil e).
j) Bestimmen Sie den Winkel, unter dem der Graph von f die y- Achse schneidet.
kann mir jemand bei irgendeiner Teilaufgabe helfen?
wirklich -13/6 x + 5x ? Nomal ist das nicht.....+5 ist eher richtig ..............kannst du ableiten und gleich null setzen ?
Oh ja tatsächlich 5. nein kann ich leider nicht so gut:(
4 Antworten
d) x=0 ( Schnittpunkte y Achse)
y=0 (Schnittpunkte x Achse )
f) Extrempunkt bedeutet Steigung ist gleich null
notwendige Bedingung f`(x) =0
hinreichende Bedingung: f"(x) kleiner null Hochpunkt
f"(x) größer Null Tiefpunkt
( h. B. aus notwendige Bedingung einsetzen Ergebniss/-e )
g) Wendepunkt bedeutet das sich die Krümmung ändert
notwendige Bedingung: f´´(x)= 0
hinreichende Bedingung f```(x) ungleich null
h) Tangente bedeutet f`(1) hat die gleiche Steigung wie Tangente bei x=1
Punkt P y Koordinate bekommst du durch f`(1) einsetzen und so hast du zwei Bedingungen und kannst die Tangenten Gleichung aufstellen.
i) beide Graphen gleichsetzen
f(x)=1/12*x³-5/8*x²-13/6*x+5
f´(x)=0=1/4*x²-5/4*x-13/6
f´´(x)=0=1/2*x-5/4
f´´´(x)=1/2 ungleich Null Wendepunkt vorhanden
a) Schnittpunkt mit der y-Achse bei x=0 f(0)=5
Nullstellen mit meinem Graphikrechner (GTR,Casio) x1=-3,7402.. x2=1,6775..
x3=9,5627..
Die erste Nullstelle muß man angenähert durch probieren ermitteln und dann einer der Näherungsformeln von Newton (Tangentenverfahren) oder Regula falsi (Sehneverfahren) verbessern.
Dann eine Polynomdivision durchführen,um auf eine Parabel zu kommen
(1/12*x³-5/8*x²-13/6*x+5) : (x-x1)=a*x²+b*x+c
x1=Nullstelle,die durch probieren ermittelt wurde.Weiter Nullstellen,wenn
0=a*x²+b*x+c
Extrema bei xmax=-1,3621... ymax=6,581.. xmin=6,3622.. ymin=-12,6227..
g) Wendepunkt f´´(x)=0 und f´´´(x) ungleich Null
h) Tangentengleichung an der Funktion f(x)=.... an der Stelle xo=..
yt=ft(x)=f´(xo)*(x-xo)+f(xo)
mit P(1/yp) → xo=1
Winkel zwischen dem Graphen f(x)=... und der x-Achse
Steigung f´(x)=m → tan(a)=m → (a)=arctan(m)
(a)=Winkel zwischen dem Graphen und der x-Achse
Infos,Herleitung der Tangenten- und Normalengleichung


d) einmal x=0 setzen -> y-Achse, y=0 setzen -> x-Achse
f) x=0 bei der ersten Ableitung
g) x=0 bei der zweiten Ableitung
h) x=1 setzen, y ausrechnen, Anstieg m am Punkt berechnen, y=m*x+n mit Bekannten Sachen füllen und n ausrechnen...
i) beide Termine gleichsetzen und alle x ausrechnen, dann noch die zugehörige. y-Werte
j) Anstieg an x=0 berechnen, Winkel draus machen
j)
entweder es ist (0/0) oder (0/5)
den punkt nenne ich (0/ys)
dann berechnet man f'(0) als Steigung und bestimmt dann arctan( f'(0) ) .