Man zeige, dass wenn f und g injektiv sind, dann ist auch g◦f injektiv?
Wie würdet ihr bei dieser Aufgabe vorgehen? Ich komme leider nicht mal auf einen Ansatz....
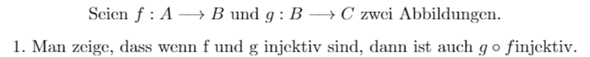
1 Antwort
Eine Funktion f ist injektiv, wenn f(x) = f(y) => x=y gilt.
Nimm als an, dass g(f(x)) = g(f(y)) gilt, für bestimmte x und y aus A.
Nutze nun die injektivität von g, und dann die von f um zu folgern dass x=y gilt. (Dies musst du nun selbst machen)
Somit ist g verkettet mit f injektiv
g(f(x)) = x^2 also nein verdammt aber ahhh dann muss ich es andersrum schreiben oder?:
g(f(x)) = g(f(y)) ---> x = y
Da g(x) injektiv ist, spielt es keine Rolle ob f(x) injektiv ist oder nicht.
g(x) = g(y) ---> x = y
Damit muss g(f(x)) = g(f(y)) ---> x = y injektiv sein, wenn g und f injektiv sind.
ahhh ja okay dann muss gellten f(x) = f(y) und da das gegeben ist, ist f°g okay gut jetzt hab ichs :D
Okay danke reicht es dann zu zeigen, dass f(x) = f(y) ---> x=y? Also:
g(f(x)) = g(f(y)) ---> x = y
Da x und y von f abhängig sind, spielt es keine Rolle ob g injektiv ist oder nicht. Außerdem wissen wir, dass f injektiv ist:
f(x) = f(y) ---> x = y