Lokale Steigungen?
Hallo, ich habe eine Matheaufgabe aufbekommen und wollte fragen, ob meine Ergebnisse stimmen.
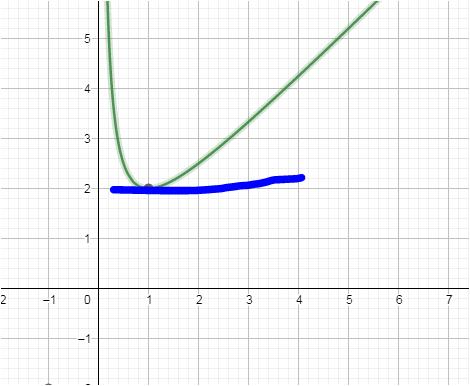
Frage: Welche Steigung hat der Graph von f an der Stelle x0?

3 Antworten
Das sieht gut aus. In der e ist ein kleiner Fehler bei der binomischen Formel. Du hast 1/2 * 2 = 2 gerechnet. Das müsste 1 sein.
Bei e) ist ein anderer Fehler in der binom. Formel: (x^(1/2)+1)²=x+2x^(1/2)+1. Das dann noch mal der 2, die vor der Klammer steht.
Bei f) verstehe ich Zeile 2 nicht! Bei der Ableitung ist das Malzeichen hinter der 1 falsch/zuviel:
f'(x)=1-x^(-2) => f'(1)=1-1=0
Dass die binomFormel immer noch so Schwierigkeiten machen , sehr vielen . Seltsam ..........Und so hinderlich für einen normalen Erfolg.
nicht guter Fehler hier

2 * ( x + 2*wurz(x) + 1 )
muss da stehen.
Die Wurzel verschwindet nur vorne , bleibt aber im Mittelteil der binomischen Formel (a+b)² = a² + 2ab + b² erhalten
.
.
da

kommt kein MAL sondern PLUS hin.
x hoch -1 albleiten :
-1 mal x hoch minus 2 = -1/x²
.
f'(x) = 1 - 1/x²
mit xo = 1
1 - 1/1² = 1-1 = 0
.
mal in den Graph schauen
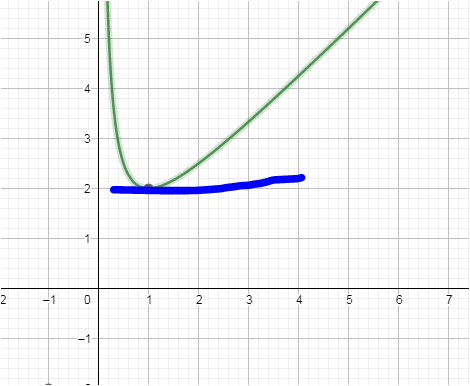
ja , bei x = 1 ist die Steigung Null ( eine waagrechte Tangente )