Logarithmus mit Wurzel?
Brauche eure Hilfe bei der Aufgabe :/ mit Erklärung bitte :)
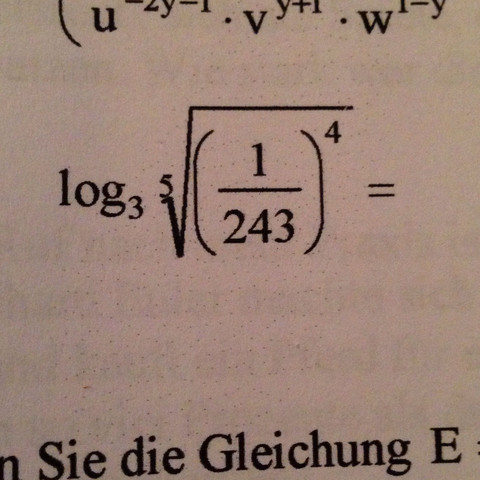
3 Antworten
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik
§1: n. Wurzeln sind nur eine andere Schreibweise für x^(1/n) also
(1/243)^(4/5)=1/81
nun natürliche log davon:
§2: log(1/81)=-log(81)=-4*log(3) da 81=3^4
nun den 3er log -> ist um Faktor log(3) kleiner als der natürliche log:
-4*log(3)/log(3)
log kürzt sich raus und über bleibt eine ganze negative Zahl...
243 = 3^5 (habe einfach mal versuchsweise in Primfaktoren zerlegt, damits leichter ist)
a-te Wurzel von x ist gleich x hoch 1/a
x hoch a hoch b ist gleich x hoch a*b
dreier Logarithmus von 3 hoch x ist gleich x
das sollte alles sein, was du wissen musst.
Die fünfte Wurzel kannst du auch als . Hoch 1 dividiert durch 5 schreiben.
Also ist das: vereinfacht:
4/5 * log3 (1/243)
Danke für deine Antwort aber kannst du bitte die Werte für a t etc. einsetzen weil ich bin leicht verwirrt :))