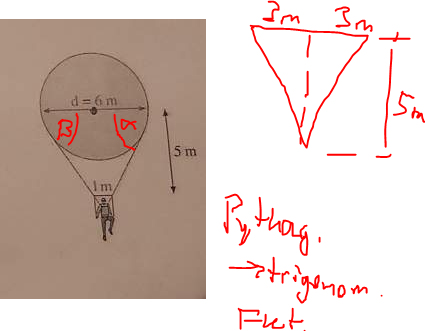
Kreistangenten Anwendungsaufgabe?

Ich weiß schon wie man die Tangentengleichung an einem Kreis von einem Punkt außerhalb des Kreises aufstellt. Ich komme aber mit dieser Frage nicht klar.
würde mich über eure Hilfe sehr freuen
Vielen Dank im Voraus!
2 Antworten
Erstmal brauchen wir die Strecke vom Mittelpunkt des Ballons bin zu dem Punkt, wo sich die Tangenten schneiden. Es sieht ja so aus, als ob die 5 Meter vom Mittelpunkt bis zu der Strebe (?) zählen, die 1 Meter breit ist. Da hilft der Strahlensatz (zweiter Teil). Es sind 6 Meter.
Dann verbinden wir den Mittelpunkt des Ballons mit dem Berührungspunkt einer Tangente. Das ist der Berührungsradius, 3 Meter lang. Der Berührungsradius ist Kathete eines rechtwinkligen Dreiecks, dessen Hypothenuse die oben berechneten 6 Meter sind. Der Sinus des Winkels zwischen der Hypothenuse und der Tangente ist 3/6, der Winkel ist also 30°.
Der gesuchte Winkel zwischen den Tangenten ist doppelt so groß, also 60°.
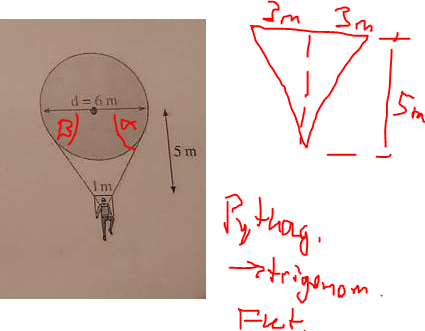
Die Aufgabe besteht darin, Alpha und Beta rauszufinden und letztendlich den Aufspannwinkel unten beim Männchen rauszufinden. (Dreieck hat immer 180° Gesamtwinkel)
Am besten versuchst du es mit Pythagoras oben, dann hast du alle Seitenlängen falls benötigt.
Dann den Sinus vom unteren Winkel bilden also: sin(y)=gegenkathete/hypotenuse
=>sin(y)= 3m/c(C ist die längste Seite)
Dann umformen und ausrechnen.
Viel Erfolg!