Tangentengleichung durch einen Punkt P, der nicht Teil von fx ist?
Guten Abend,
Die Aufgabenstellung lautet:
Bestimmen Sie die Gleichung der Tangenten an den Graphen von f, die durch den Punkt P(1|1) verläuft. f(x)=2x/(x-2).
Da f selber nicht durch P verläuft, lässt sich keine Tangentengleichung nach normalem Schema aufstellen. So habe ich nun aber schon so ziemlich jede Methode probiert und Formeln x-Mal umgestellt, um auf den Punkt Q von f(x) zu kommen, der von einer Tangente geschnitten wird, die gleichzeitig durch P verläuft.
Daher wäre ich über Hilfe sehr erfreut.
VG und Danke im Voraus.
3 Antworten
So habe ich nun aber schon so ziemlich jede Methode probiert ..
Das kann ich mir gut vorstellen, denn die Lösung ist nicht trivial und rein analytisch kaum zu finden. Aber ich liebe solche mathematischen Knobeleien. ....und es gibt eine Methode, um die Lösung zu finden:
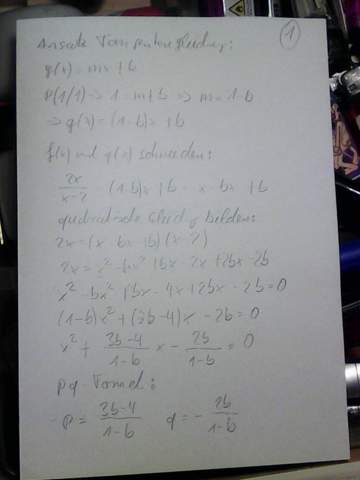

statt mit einem Funktionenplotter könnte man die Nullstellen für b auch mit irgendeinem numerischen Näherungsverfahren finden.
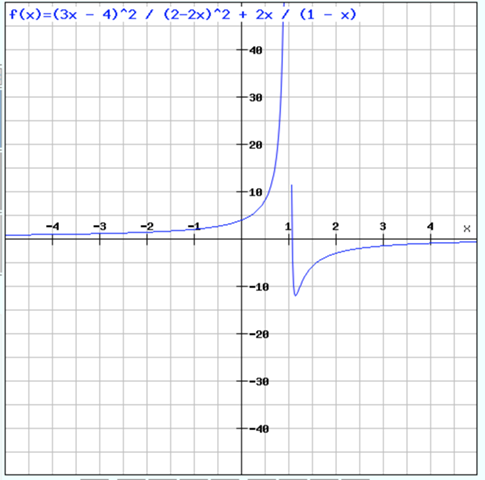
Hier der Überblick über die Funktion von b:
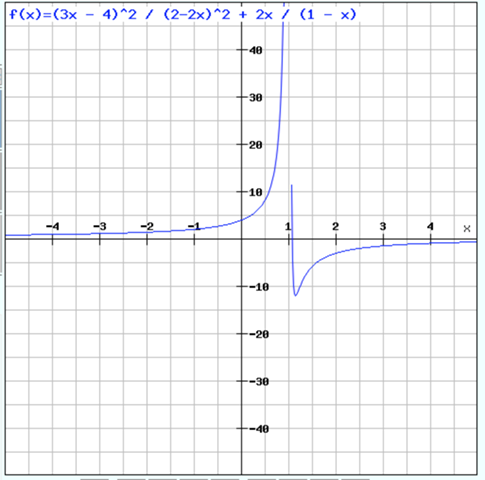
sofort zu sehen: es gibt nur ein Nullstelle für b und damit auch nur eine Tangentengleichung.
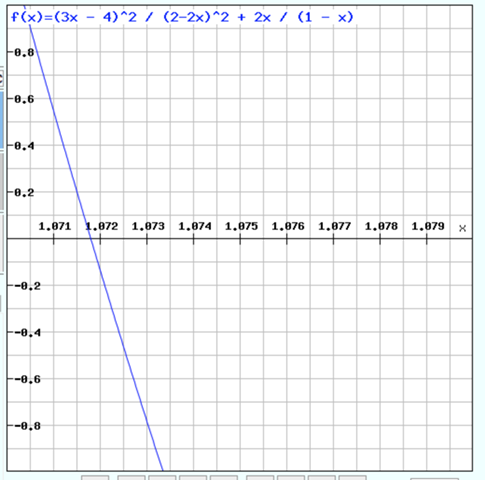
Dasselbe nochmal mit hoher Auflösung, um b besser ablesen zu können:
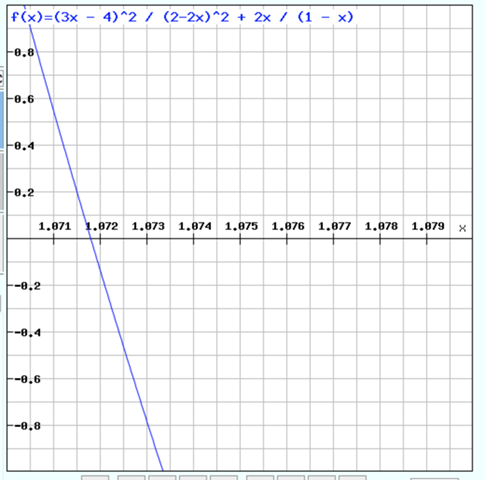
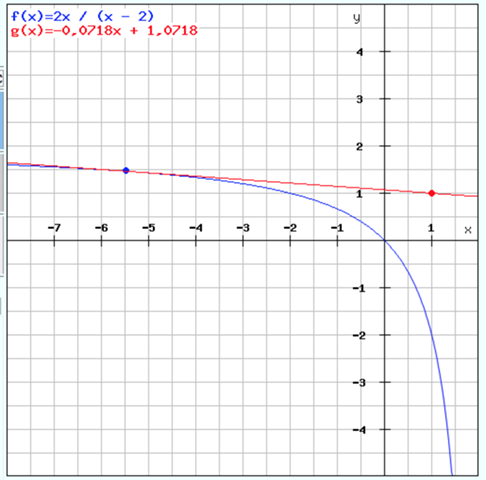
und hier der Plot von der Lösung:
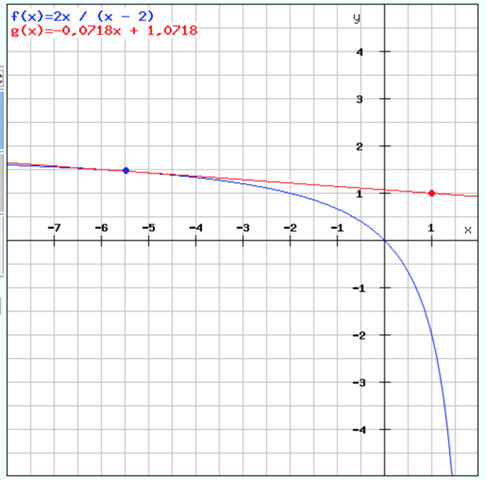
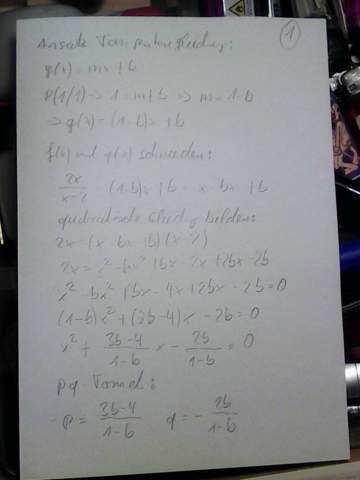

Hut ab, das ist eine sehr elegante Lösung durch die p/q Formel und definitiv angenehmer als die langwierige und sehr zeitintensive, die ich genutzt habe! Deshalb auch hier nochmals meinen ausdrücklichen Dank!
Hi,
schau mal hier:
https://abiturma.de/mathe-lernen/analysis/tangenten/tangente-durch-fernpunkt
kommst Du damit weiter?
Darfst gerne fragen!
LG,
Heni
Was hast du denn schon probiert? Zeige uns das doch mal.
Die Ableitung f'(x) ist ja klar -4/(x-2)².
Allgemeine Tangentengleichung wäre folglich also:
-4/(x-2)² * (x - x0) + y0, wobei x0 und y0 die Koordination des Punktes Q wären. Um später durch Punkt 1|1 zu verlaufen habe ich mir gedacht, dass dahergehend selbstverständlich diese Funktion bei x=1 y=1 ergeben muss. So hätte man nach mehreren Umformungen die Gleichung 1= -4/(x-2)² * x0-1 + y0. Weiter komme ich leider nicht, da hier schließlich zwei Variablen vorliegen... Hoffe, dass das so ersichtlich ist, denn ein Bild würde ich von meinen schemenhaften Ansätzen eher ungern hochladen ^^
Der Ansatz ist gut und prinzipiell richtig. Allerdings musst du aufpassen. Bei einer Geradengleichung kann x nie im Nenner stehen wie es bei dir der Fall ist. Da liegt also was im Argen. Denn du hast ja als Steigung m geradef'(x0) = -4/(x0 - 2)^2. Jetzt noch zusätzlich fordern dass die Gerade durch (1|1) geht und du solltest eine Unbekannte eliminieren können. Probiere also noch mal. Die Aufgabe ist nebenbei nicht einfach, toll dass du den richtigen Ansatz gefunden hast.
In der Tat! Ich habe ebenfalls die ganze Zeit weitergegrübelt, wie man y0 wegbekommen könnte. Da fällt es einem ja wie die Schuppen von den Augen. y0 ist ja nichts weiteres als f(x0), d.h. man kann den Funktionsterm einfach nochmal hinschreiben und hat so nur noch eine Variable, nämlich x0! Dann x0 in die ganzen Polynome einsetzen, zusammenfassen und auflösen und so erhält man zwei x0-Werte! Mit denen kann man dann die Tangentengleichungen einfach normal ausfüllen und x als Variable belassen, die ja bei x=1 y=1 ergeben muss. So kommt man bei f(x) dann zur Tangentengleichung ft(x)=(-7+4*sqrt(3))*x+8-4*sqrt(3). Das passt, tangiert f(x) an einer Stelle und durchquert 1|1. Aufgabe gelöst, würde ich sagen. Vielen Dank für deine Hilfe!
Vielen lieben Dank!
Der Artikel war äußerst hilfreich! Zwar geht es in diesem nur um Parabeln und Tangenten die dort Fernpunkte durchschneiden, aber man konnte trotzdem den zündenden Punkt rauslesen, der mir geholfen hat, die Aufgabe zu lösen :). Daher nochmals danke sehr!