Kovarianz berechnen?
Im zweimaligen Wurf eines fairen Würfels sei X das Ergebnis des ersten Wurfes, Y das Maximum sowie Z das Minimum der beiden Würfe.
Ich soll nun die Kovarianzen Cov(X,Y), Cov(X,Z) und Cov(Y,Z) berechnen. Ich kenne auch die Formel, weiß aber nicht, wie ich E[X*Y] etc berechne. Kann mir bitte jemand helfen?
Davor habr ich schon eine Kontingenztafel gezeichnet für Y,Z und deren Erwartungswerte berechnet.
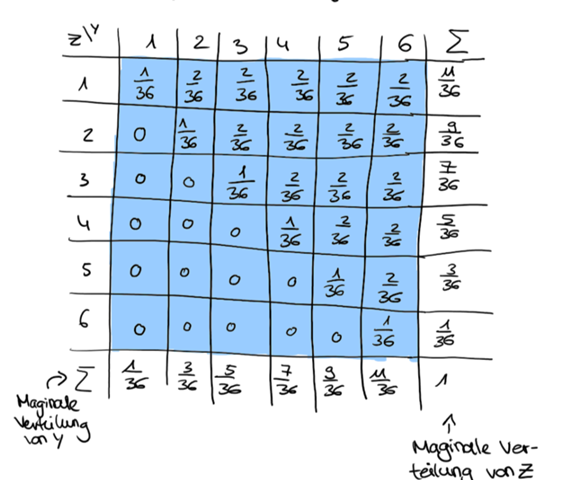
die Tafel für Y,Z
2 Antworten
Wenn du schon für Y,Z eine Kontingenztafel gemacht hast, kannst du das genauso für X•Y etc machen: Auf einer Achse Ergebnis des ersten Wurfes, auf der anderen das Ergebnis des zweiten Wurfes, die Werte für X•Y eintragen, zusammenzählen und durch 36 teilen.
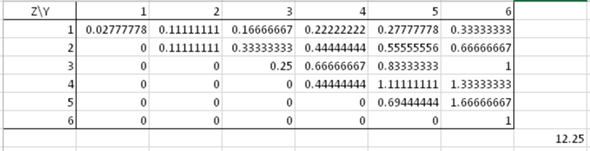
Tabelle aus Ergänzung multipliziert mit Y ⋅ Z und aufsummiert = 12,25 = 441/36
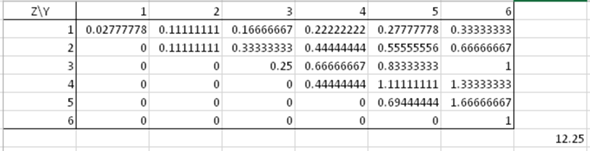
Also ich habe halt die Lösung, aber verstehe einfach nicht, wie die auf diese Zahlen gekommen sind. Ich kann es mal hochladen, wenn du dich damit auskennst?
aber welche Einträge womit denn? Da steht ja so viel drin, hab ein Bild hochgeladen
Ahh okay danke. Und dann male ich mir für jede Kovarianz wieder ne Tabelle? Also für X,Y zb. Dachte das wären weniger Rechenschritte als diese 36 Einträge :D aber danke, dann rechne ich jetzt mal los!
Ich komme leider auf ein falsches Ergebnis..
Was rechnest du?
Bei Y*Z ist es übrigens leicht. Da kommen nämlich automatisch immer beide Würfelzahlen vor. Y, Z sind also unabhängig und der Erwartungswert des Produktes somit das Produkt der Erwartungswerte.
Ich habe 1*1*1/36+.. gerechnet, also für alle Einträge. Ist das richtig?
Mit einem Summanden ist das schwierig vorherzusagen. Ich bekomme 441/36.
Das ist was anderes. Ich habe die Tabelle zur Rechnung in meiner Antwort ergänzt.
Aber 441/36 ist doch gekürzt 49/9 und das ist 12,25
Ich glaube die Person hat sich verschrieben und meint 49/4?
Ich habe mich verschrieben, ich hatte tatsächlich 49/9 raus.
Wurf
4 6
erzeugt
x y z x*y
4 6 4 24
.
5 1
erzeugt
5 5 1 25
.
E(xy) = 1/36 * ( 24 + 25 +++++ )
.
geht ja sogar einfacher : Wiki EW
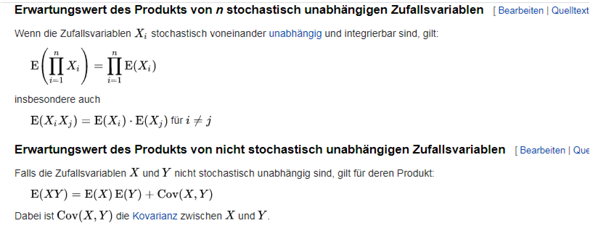
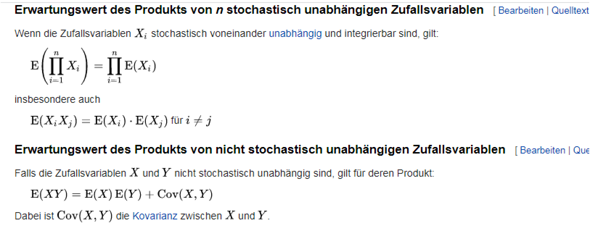
Ich verstehe es leider noch nicht. Ich versuche mich gerade an Cov(Y,Z) und habe die Lösung, aber wie komme ich bei E(Y*Z) auf 266/36? Kannst du mir das vllt Schritt für Schritt erklären?
aber ich bekomme es auch mit der Kontingenztafel irgendwie nicht hin..