Korrekt?
Ich will es verstehen, die gestreckten und gespiegelten habe ich verstadnen wie sie zu erkennen sind, aber die Verschiebungen weiß ich nicht, also ich weiß bei den verschobenen nur, dass die minus Zahl plus wird und auf die positive verschoben wird und umgekehrt, aber wie ich sie graphisch erkenne und wieso die anderen nicht stimmen würde ich auch noch wissen..., ich wäre dankbar für eine Erklärung.
1 Antwort
Eine Funktion wird um a Einheiten nach rechts verschoben, indem man f(x-a) rechnet; a Einheiten nach links entsprechend mit f(x+a).
Hier soll g(x)=f(x-2) gelten, d. h. der Graph von g ist um 2 Einheiten nach rechts verschoben. D. h. z. B. g(3)=f(3-2)=f(1), und das heißt: den y-Wert, den f bei x=1 hat, hat g erst bei x=3 (also 2 Einheiten weiter rechts). Am besten erkennt man das, wenn man sich markante Punkte von f anschaut, z. B. Null- oder Extremstellen und anschließend guckt, an welcher x-Stelle diese beim verschobenen Graphen sind.
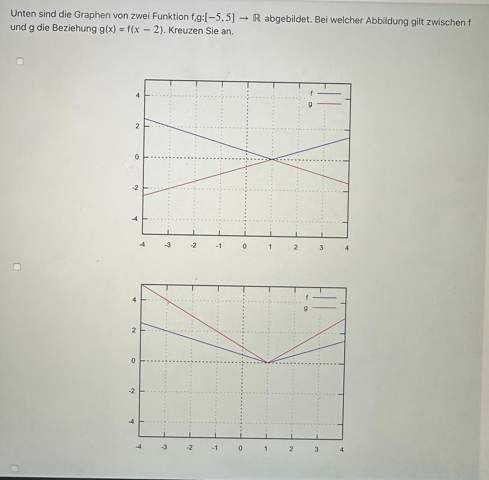
In Bild 1 ist g gegenüber f an der x-Achse gespiegelt, also g(x)=-f(x).
In Bild 2 ist die Nullstelle dieselbe, d. h. hier liegt wieder eine Streckung vor: g(x)=a*f(x).
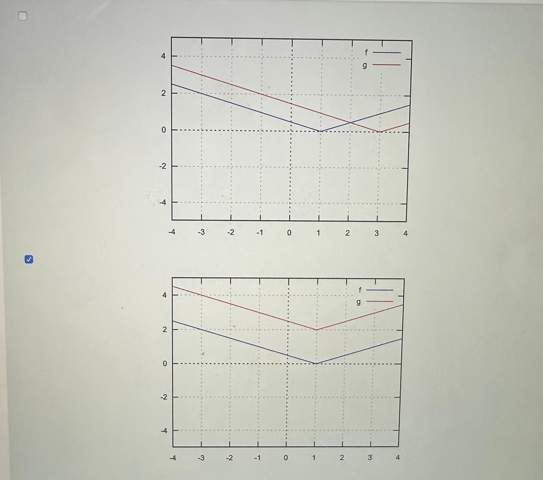
In Bild 3 hat f bei x=1 seine Nullstelle - die von g ist bei x=3, also 2 Einheiten weiter rechts, also g(x)=f(x-2), also der geforderte Graph!!!
In Bild 4 liegen die Tiefpunkte übereinander, wobei der von f gleichzeitig Nullstelle ist, d. h. g wurde in y-Richtung verschoben, also g(x)=f(x)+c (in diesem Fall c=2).
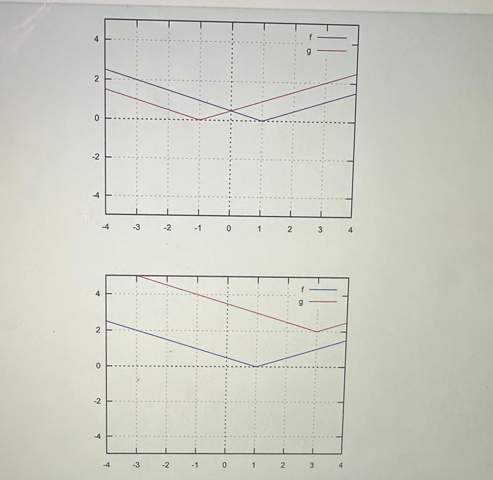
In Bild 5 ist die Nullstelle von f wieder bei x=1, die von g aber bei -1, also 2 Einheiten weiter links, d. h. hier gilt g(x)=f(x+2).
In Bild 6 verlaufen die Geraden jeweils parallel. Der Tiefpunkt von g ist 2 Einheiten weiter rechts und 2 Einheiten weiter oben, d. h. hier gilt g(x)=f(x-2)+2.
Danke auch - wichtiger als der Stern ist mir, dass Du es verstehst! :)
Vielen Dank! Hast den Stern verdient, echt super!!!! 👍🏻