Komplexe Wahrscheinlichkeitsrechnung?
Ich wollte mal wissen, wie ich die Wahrscheinlichkeit berechne, dass ein Ereignis mit einer bestimmten Wahrscheinlichkeit nach einer bestimmten Anzahl an versuchen mehrmals eintritt.
also zum Beispiel dass Ereignisse hat eine 0.11% wahrscheinlich wie wahrscheinlich ist es nach 250 versuchen 3x dieses Ereignis zu bekommen
Ich freue mich auf Antworten. Bei Fragen könnt ihr euch gerne melden.
5 Antworten
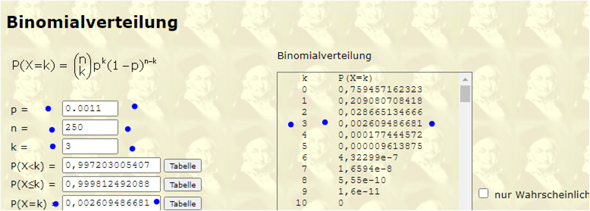
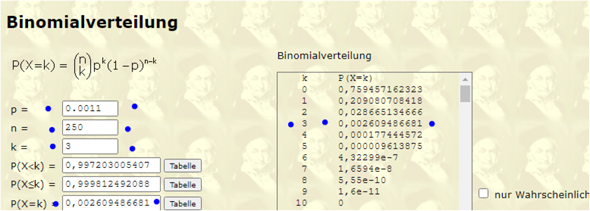
ich übersetz mal : Es gibt ein Glücksrad und ein Feld hat eine W von 0.11% , mathematisch w = 0.0011
Es wird 250 mal gedreht.
Wie groß ist die W , dass GENAU dreimal dieses Feld kommt .
.
Dat geht mit einem Rechner für Binomialverteilung ( bi = zwei , entweder das Feld oder zu 1 - 0.0011 das Feld nicht )
.
Der liebe Arndt Bruenner hat es für uns alle programmiert
ca 0.26 % kommt raus .
Deine Frage ist etwas unpräzise. Ich weiss nicht, ob es dir darum geht, dass die ersten 250 Versuche einen Einfluss auf die folgenden 3 haben. Ich nehme mal an, dass du von stochastisch unabhängigen Ereignissen ausgehst. Dann gibt es diesen Einfluss nicht. Man kann die Frage dann auf folgende Arten verstehen:
(1) Erst eine Reihe von 250 Versuchen, Ergebnis egal, dann 3 aufeinanderfolgende Treffer. Dann kommt es auf die ersten 250 Versuche gar nicht an, die Wahrscheinlichkeit ist (0.11%)^3.
(2) Erst 250 Nieten, dann 3 Treffer, die Wahrscheinlichkeit ist (1-0.11%)^250 * (0.11%)^3
Unter der Annahme, dass die Versuche Stochastisch unabhängig voneinander sind, kannst du das Experiment mit einer Binomialverteilung mit 250 Versuchen mit Erfolgswahrscheinlichkeit 0.0011 modellieren.
Nutze dann die Formel für die Binomialverteilung um die Wahrscheinlichkeit für 1 bzw 3 Erfolge zu bestimmen.
(99.98%)^250*(0.11%)^3≈0.00000101%
1 Treffer:
250x0,0011=0,00275
3 Treffer:
0,00275x0,00275x0,00275 =
2,0796875E-08
In Prozent:
2,0796875E-6
also es ist wie bei ein Glücksrad und nach 250 mal drehen ist es insgesamt 3 mal auf das Feld mit einer 0.11% wahrscheinlich gekommen.
Ich entschuldige mich wenn es unklar wahr