Integration durch substitution, konstanter Faktor rausziehen?
Kann man den vorfaktor 1 nicht einfach vor das integral ziehen? So verwendet wie in dem Video wäre die Stammfunktion von cos(x) ja auch anstatt sin(x) :
Integral(1*cos(x)) =
x * cos(x) - Integral(x * (-cos))
--> Integral(x * (-cos)) =
cos (x) * x - Integral( cos (x) * 1) =
==>
Integral(1 * cos(x)) =
x * cos(x) - cos (x) * x -
Integral( cos (x) * 1)
<=>
2 * Integral(1 * cos(x)) =
x * cos(x) - cos (x) * x
Teile ich den unteren Ausdruck durch 2 habe ich da doch nur noch 0 stehen
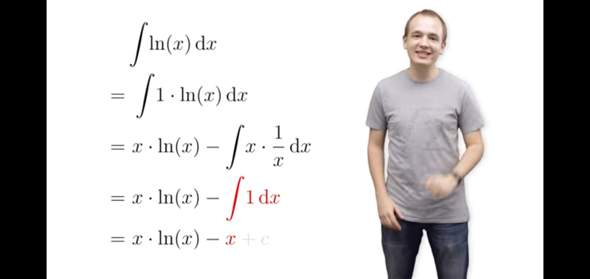
Und ich denke (x * cos(x) - cos (x) * x)/2 ist keine Identität aus der sich irgendwie sin(x) ergibt oder?
3 Antworten
Du meinst wohl partielle Integration, und bei deinem Ansatz müsste es eher heissen
Integral( 1 * cos(x) ) =
x * cos(x) - Integral( x * (-sin(x)) )
Der Trick aus dem Video geht hier nicht. Und wenn man hier schon wissen muss, dass die Ableitung des cos der -sin ist, dann brauchte es auch nicht viel Grips um darauf zu kommen, dass die Stammfunktion des cos der sin ist.
Hallo,
dieser Faktor 1 wird je gerade deswegen benötigt, weil man das Integral von ln(x) erst herleiten muß.
Durch Anwenden der partiellen Integration findet man die Stammfunktion von ln(x), ohne sie vorher zu kennen. Es reicht, die Ableitung von ln(x) zu bilden.
Herzliche Grüße,
Willy
Also wenn ich in meiner Beispielrechnung jetzt einfach mal annehme ich wüsste das die Ableitung vom -cos der -sin ist folgt:
--> Integral(x * (-cos)) =
1 * (-cos) - Integral(1 * (-sin))
==>
Integral(1*cos(x)) =
x * cos(x) - Integral(1 * (-sin))
(Jetzt nehme ich auch noch an ich wüsste schon das (-sin) aufgeleitet cos(x) ist. ==>
Integral(1*cos(x)) =
x * cos(x) - cos(x)
cos(x) (x-1)
Das ist jetzt merkwürdig, sieht aus wie ne Identität ist es aber nicht :(
Also scheinbar reicht es nicht aus an dieser Stelle zu wissen was die Ableitung ist und dann so zu tun als würde man die restlichen in Kreis aufkommenden Stammfunktionen kennen um dann drauf zu schließen.
....
Oder ich habe mich verrechnet, aufjedenfall mache ich mir jetzt erstmal n Kaffee und lasse es sein damit zu spielen, danke!
Ich wollte sozusagen eine direkte Integration überspringen, dann über 1x Schritt substitution und alles folgende durch direkte Integration auf die richtige Integration der Trigonometrischen Funktion kommen
Weise nach, daß der Kosinus die Ableitung vom Sinus ist.
Daraus ergibt sich dann automatisch, daß der Sinus eine Stammfunktion des Kosinus ist. Der Nachweis erfolgt über den Grenzwert des Differenzenquotienten.
Wie das geht, kannst Du im Netz finden. Ist etwas tricky, aber gut nachzuvollziehen.
https://matheguru.com/differentialrechnung/beweis-fur-die-ableitung-von-sinx.html
Und ansonsten würde ich so entweder unendlich weiter integrieren oder auf einen Ausdruck kommen der offensichtlich nichts bringt?
(x * cos(x) - cos (x) * x)/2 = 0
Also ist hier die entscheidende Stelle, dass man zum Glück das x im integral der 3. Zeile (video) kürzen kann?