Hat die Funktion f(x) = ln(x)-x eine schräge Asymptote?
Frage oben in Beschreibung.
Ich hätte nein gesagt, da der lim von ln(x) für x gegen inf = + inf ist und nicht beispielsweise eine Zahl.
Allerdings wird ja auch der Zuwachs von ln(x) pro delta x immer kleiner, was mich unsicher macht.
Also formal meine ich:
[ Sei g(x) = ln(x), so ist g'(x) = 1/x ]
Der lim von g'(x) für x gegen inf ist 0.
Danke im Voraus,
BuzzaFrund
3 Antworten
Nein. Die durch f(x) = ln(x) - x reelle Funktion hat keine schräge Asymptote. D.h. es gibt keine Asymptote der Form y = a ⋅ x + b (mit a ≠ 0).
Dafür müsste nämlich die Differenz (ln(x) - x) - (a ⋅ x + b) gegen 0 konvergieren (wenn x gegen einen Randpunkt des Definitionsbereiches geht, im konkreten Fall also x → 0 bzw. x → ∞). Jedoch ist...
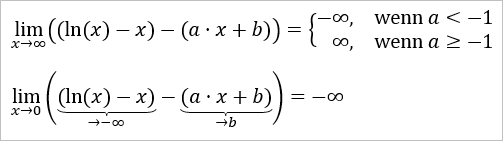
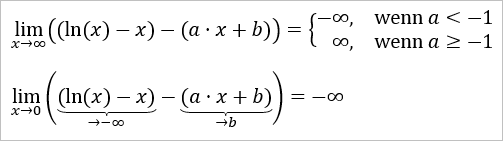
Danke! Das ist verständlich und logisch begründet.
Aber ist es für diesen konkreten Fall nicht eigentlich irrelevant, was die Differenz macht, wenn x -> 0, weil die Asymptote sich ja erst für x-> inf zu erkennen gibt.
überraschend finde ich aber ,dass die Fkt als Graph den Eindruck einer Geraden macht ............ein paar Fkt - Werte.........
ln(1000) = 6.90 - 1000
ln(10000) = 9.21 - 10000
ln(100000) = 11.51 - 100000
ln(10 hoch 100) = 230.25
das ist nun Bastelei , aber es ist so , also ob die Differenz immer größer wird
ln(x) ist ein Exponent, der mit e als Basis x ergibt .
Da e = 2.718........müssen alle Exponenten beginnend ab unter +1 kleiner sein als x .
Also dominiert langfristig -x in der Fkt und y = -x ist Asymptote .......ob das als Beweis ausreicht , weiß ich nicht.
man müsste zwingender zeigen , das ln(x) < x ist .
Der Limes von ln(x) - x für x gegen +unendlich ist -unendlich, da eben der Logarithmus deutlich langsamer wächst als x.
Ich kannte den Begriff der schrägen Asymptote so noch nicht (spielt auch in höherer Mathematik keine wirkliche Rolle). Aber wenn ich mir das hier
https://www.studienkreis.de/mathematik/asymptoten-funktionen/
so anschaue würde ich sagen f hat keine schiefe Asymptote.
Jetzt kann ich dazu nur sagen : da -x reelle Asymptote ist ,muss deine Schlussfolgerung irgendwie einen Haken haben !
@Halbrecht Das waren zwei verschiedene Fälle. Aber das hat sich ja jetzt alles durch die Antwort von mihisu geklärt.
Ja klar, das habe ich auch nicht gemeint.
Ich meinte: wenn die Fkt zB. f(x) = 1/x - x heißen würde, dann hätte diese definitiv eine schräge Asymptote weil lim x->inf 1/x = 0. Damit ist die schräge Asy y=-x
Da jedoch bei f(x) = ln(x)-x gilt lim x-> inf ln(x) = + inf, folgere ich daraus, dass f(x) keine schräge Asymptote hat. Stimmt das?