Globalverhalten ganzrationaler Funktionen?
Hallo, ich habe im Unterricht momentan das oben stehende Thema und ich verstehe wirklich 0! Was bedeuten denn überhaupt x = unendlich und x= - unendlich ???????? Und wie kann ich das Verhalten an Funktionen untersuchen???? Bitte erklärt es mir ausführlich oder gibt mir einen Link für ein Video.
Danke im voraus.
2 Antworten
man möchte den groben Verlauf der Funktion untersuchen;
von wo kommt sie links und wo geht sie rechts hin? (unmathematisch ausgedrückt)
zB f(x) = x³ -2x+4
sie kommt von links unten und geht nach rechts oben,
denn
(-oo)³ = -oo
(+oo)³ = +oo
oo = unendlich
Das Globalverhalten nennt man auch Unendlichkeitsverhalten. Dabei untersucht man, wie sich der Graph der Funktion im Unendlichen verhält. Wir wollen also wissen, ob der Graph ganz weit rechts, also im positiven unendlichen Bereich der x-Koordinaten nach oben oder unten verläuft. Ebenso gilt das auch für den Bereich ganz weit links, also den negativen unendlichen Bereich der x-Koordinaten.
Deswegen setzen wir einmal positiv und einmal negativ unendlich ein. Allerdings kann man so nicht mit dem Begriff unendlich rechnen. Deswegen nutzen wir im Kopf einmal hohe negative und hohe positive Werte.
Das Verfahren schreibst du mit dem limes (Grenzwert) auf.
Unter lim f(x) ... steht dann x--> +∞ und einmal eben x--> -∞.
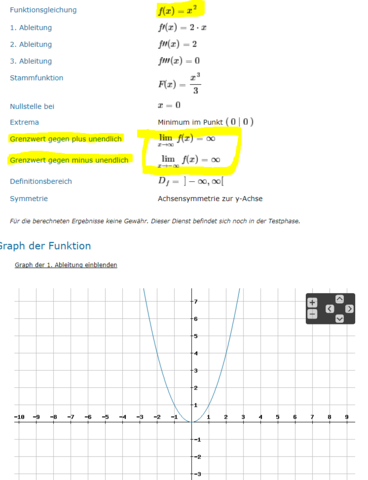
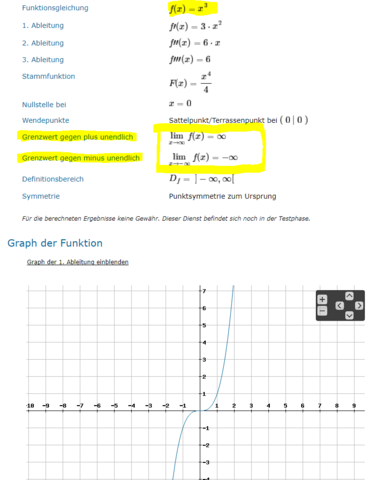
Schau dir dazu bitte schon einmal die Bilder an. Im gelb eingerahmten Bereich siehst du das.
Du musst dabei allerdings auch oft mit mehr als nur dem Taschenrechner rechnen, der oft eher ein Hilfsmittel ist. Viel eher musst du die Werte im Kopf einsetzen und schauen, welche Klammern und Faktoren positiv und negativ werden würden. Spätestens bei den speziellen Exponentialfunktionen, den e-Funktionen, wird der Taschenrechner nicht mehr viel nützen. Dort wirst du dann nämlich öfters mal merken, dass am Ende sowas wie positiv unendlich mal null dort steht. An sich ist etwas mal null ja immer null. Beim unendlichen sieht das aber eben in solch einem Fall wieder anders aus. Hier gilt: Das e (also die Euler'sche Zahl) dominiert! wäre das positiv unendliche dann also das e^x, würde die Funktion eben gegen positiv unendlich, nicht gegen null laufen. Das musst du aber noch nicht verstehen, das kommt alles später noch, wahrscheinlich im Abiturjahrgang.
Beispiele (siehe auch Bilder):
- f(x) = x²
Setzen wir hier hohe positive oder negative Werte ein, bekommen wir immer positive Werte raus. Denn das Quadrat sorgt dafür, dass auch negative Werte mit sich selbst multipliziert wieder positiv werden, da Minus mal Minus wieder Plus ergibt. Die Funktion f verläuft also sowohl im positiven als auch negativen unendliche Bereich gegen positiv unendlich (im Sinne der y-Koordinaten).
Anders wäre das bei der Funktion:
- f(x) = x³
Hinweis:
(-) * (-) * (-) = (-)
Setzten wir etwas negatives ein, kommt auch etwas negatives raus. Setzen wir etwas positives ein, bleibt es positiv.
Somit verläuft die Funktion im negativen unendlichen (also links) gegen negativ unendlich, also nach unten. Im positiv unendlichen verläuft sie gegen positiv unendlich, also nach rechts oben.
Schau dir dazu bitte beide Bilder genau an. Spätestens dann solltest du es verstehen. Die Screenshots habe ich von folgender Seite gemacht, welche dir das Unendlichkeits- bzw. Globalverhalten auch berechnet:
http://funktion.onlinemathe.de/
_________________________________________________________
Bei Fragen einfach melden! :)
Liebe Grüße
TechnikSpezi