Mathe Globalverhalten von e-Funktionen?
Hallo ihr Lieben,
in Mathe haben wir letzte Stunde das Globalverhalten besprochen.
Leider verstehe ich dies überhaupt nicht und bald steht auch schon die Matheklausur an...
Könnte mir eventuell jemand dies anhand der beiden unten stehenden Funktionen erklären?
f(x)=e hoch 3x
g(x)=xe hoch x
Liebe Grüße und danke im Voraus!
flowerpowerfee
3 Antworten
Globalverhalten untersuchen bedeutet, Du musst die Grenzwerte (lim) für x gegen plus- und minus-unendlich berechnen.
Dazu setzt Du für x einmal sehr hohe positive und einmal sehr negative Werte ein (entweder im Taschenrechner oder gedanklich).
Bei e^x wird die gesamte Potenz für steigende x natürlich immer größer: der Exponent gibt an, wie oft man die Basis mit sich selbst multiplizieren muss; ist die Basis größer als 1 (e=2,718...), dann steigt natürlich auch das Produkt, wenn man immer wieder mit einer Zahl größer als 1 multipliziert.
Ist nun x negativ, d. h. der Exponent ist negativ, dann "wandert" die Potenz in den Nenner mit positivem Exponenten, d. h. e^(-x)=1/e^x. Für negative x-Werte gilt also bei Deinen Funktionen f(x)=1/e^|x| und x<0. Wird nun der Betrag von x immer größer, dann wird der gesamte Bruch immer kleiner, d. h. der Bruch läuft Richtung 0.
Bei Deiner Funktion g(x) hättest Du somit für x gegen minus-unendlich die Funktion:
g(x)=x/e^|x|, d. h. bei Betrachtung des Grenzwertes lim g(x) = x/e^|x| = minus-unendlich durch plus-unendlich.
Nun ist es so, dass Exponentialfunktionen deutlich schneller steigen als "normale" Polynomfunktionen, d. h. hier steigt der Nenner deutlich schneller als der Zähler, somit ist der Grenzwert für x->minus-unendlich gleich Null (der Graph läuft unterhalb der x-Achse Richtung Null, da ja der Zähler negativ ist, während die Potenz im Nenner immer positiv ist).
Das ist erst einmal wie bei allen anderen Funktionsarten vorher auch. Es gibt nur wenige spezielle Dinge, die du dabei neu lernen musst.
f(x) = e^(3x)
Setzte (hohe) negative Werte für x ein (x --> -∞):
f(-1) = e^(3*(-1))
f(-1) = e^(-3)
Das wird aber keine negative Zahl, sondern eine sehr kleine, die immer weiter an die null geht.
e^(-3) ist das gleiche wie 1/e³.
Je höher also die eingesetzte Zahl, desto größer würde der Nenner und damit um so kleiner der Bruch werden. Die Zahl wird aber nie negativ, denn e^x ist immer größer null. Egal wie oft ich die eigene positive Zahl mit sich mal nehme, da wird nie etwas negatives raus. Auch nicht, wenn der Exponent selbst negativ ist.
Wir sehen also:
Wenn wir x gegen -∞ laufen lassen, verläuft der Graph asymptotisch zur x-Achse. Je weiter man also auf der x-Achse nach links geht, desto näher kommt der y-Wert an die null ran.
Die Asymptote ist also bei y=0 und somit ist es die x-Achse selbst.
_______________________________
Setzte (hohe) positive Werte für x ein (x --> +∞):
f(1) = e^(3*1)
f(1) = e³
f(2) = e⁶
Hier ist es nicht schwer: Die Zahl wird natürlich immer größer.
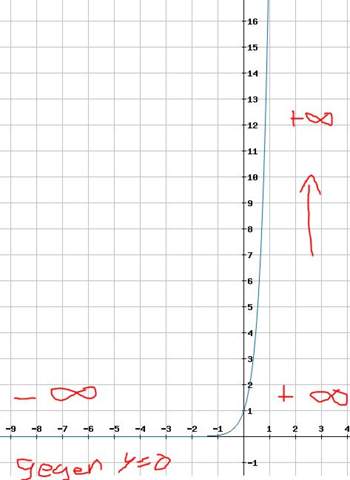
Wenn wir x gegen +∞ laufen lassen, verläuft der Graph also auch ins positiv unendliche der y-Werte, also nach oben.
Das kannst du hier auch nochmal alles sehen:
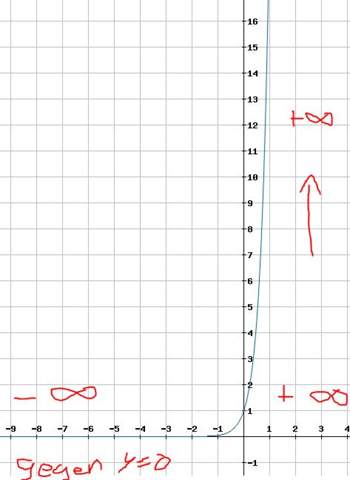
Aufschreiben kannst du das z.B. so:

Liebe Grüße
TechnikSpezi

Hier muss man wissen, wie sich einige Standardfunktionen (in etwa die Exponentialfunktion bei deinen Beispielen) für sehr große und sehr kleine (also sehr stark negative) x-Werte verhalten. Weißt du das zufälligerweise? Welchen Wert nimmt die Exponentialfunktion e^x für sehr sehr große x-Werte x->oo an? Und welchen für x-> -oo?
Ich hab leider gaaaar kein Plan von Mathe :D das einzige was ich verstehe ist das hier: https://www.abiweb.de/mathematik-analysis-1/funktionsuntersuchung-ganzrationaler-funktionen-teil-2/globalverhalten.html, aber das kann ich ja leider nicht gebrauchen, da das ja nichts mit e-Funktionen zutun hat
Ich denke mal, wenn x gegen plus unendlich, dann ist f(x) = unendlich und wenn x gegen minus unendlich, dann ist f(x) = null
Genau, super!
Und jetzt müssen wir noch verstehen, was sich ändert, wenn wir die Funktion f(x)=e^(3x) betrachten statt f(x)=e^x. Hast du jetzt vielleicht einen Verdacht, wie es da ausschauen könnte?
Wahrscheinlich wird es genauso aussehen, da 1 und 3 ja beides ungerade Zahlen sind und bei beidem ein positives Vorzeichen vorliegt. Wenn ich das so richtig verstehe
Du kommst auf das richtige Ergebnis, obwohl ich mir nicht ganz sicher bin, ob du auf dem richtigen Weg dahin gekommen bist. Es kommt nicht darauf an, dass 1 und 3 ungerade sind, auch für h(x)=e^(4x) würde noch dasselbe gelten, obwohl 4 gerade ist.
Die Idee ist hier folgende: Du kannst die Funktion f(x)=e^(3x) schreiben als f(x)=e^y(x) mit y(x)=3x. Nun geht für x gegen oo auch y(x) gegen oo. Genauso geht y(x) gegen -oo, wenn x gegen -oo geht. Du siehst also, das Multiplizieren mit 3 hat keinen Effekt, wenn wir nur an diesen Grenzwerten interessiert sind. Also wird sich f(x)=e^(3x) genauso verhalten, wie e^x. Macht das Sinn?
Ok, kein Problem! :) Schau dir mal den Graphen der e-Funktion an: https://de.wikipedia.org/wiki/Exponentialfunktion#/media/File:Exp_e.svg
Was denkst du, gegen welchen Wert strebt die e-Funktion, wenn x sehr groß wird?