Formel von Binet verstehen?
Hallo zusammen. Ich muss gerade in meiner Probeprojektarbeit für die Schule über die Fibonacci-Folge die Formel von Binet erkären. Aber irgendwie finde ich nirgendwo sinnvolle Quellen oder verständliche Erklärungen.
Kann mir jemand eine Erklärung + Quelle oder irgendetwas anderes hilfreiches zum Thema liefern?
Vielen Dank für jede Antwort
1 Antwort
Anfangs waren die Fibonacci-Zahlen rekursiv definiert (fₙ = fₙ₋₁ + fₙ₋₂ ∧ f₁ = f₂ = 1, wobei fₙ = n.te Fibonacci-Zahl), aber das Problem hierbei ist, dass wir nicht direkt ausrechnen können, was die n.te Fibonacci-Zahl ist: Wir müssen zuerst alle davor liegenden Fibonacci-Zahlen bestimmen. Wir nennen das auch inexplizit. Das macht es zeitaufwendiger große Werte zu berechnen.
Z.B.:
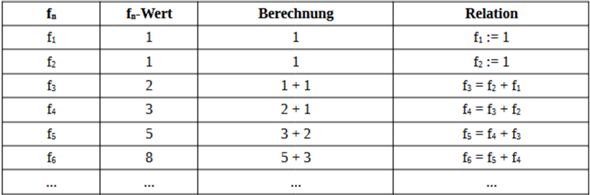
Die Formel vom Binet soll hier Abhilfe schaffen. Sie ist explizit. Das bedeutet: Wir setzen einfach nur "n" ein und erhalten direkt den exakten Wert:
Einfach nur einsetzen und zack hast du das Ergebnis.
Das hat noch weitere Vorteile, z.B. kannst du mit f(n) = fₙ, die Zahlen auf einer stetigen und differenzierbaren (keine Löcher und keine Zacken) Kurve darstellen. Du kannst die Fibonacci-Zahlen auch damit verallgemeinern, was beim Vereinfachen oder finden von expliziten Relationen nützlichen sein kann.
Nette Quellen:
Chandra, Pravin and Weisstein, Eric W. "Fibonacci Number." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/FibonacciNumber.html