Fehler bei vollständiger Induktion?
Habe ich beim Induktionsschritt einen Fehler gemacht? (oder generell irgendwo einen?) Denn ich komme nicht mehr voran. Lerne erst gerade über das Induktionsprinzip. Kann mir wer bitte helfen? Danke!
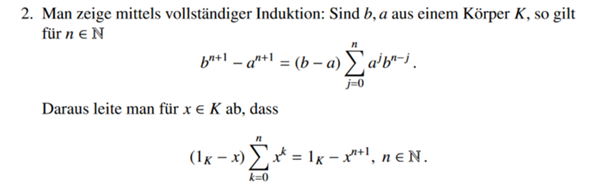
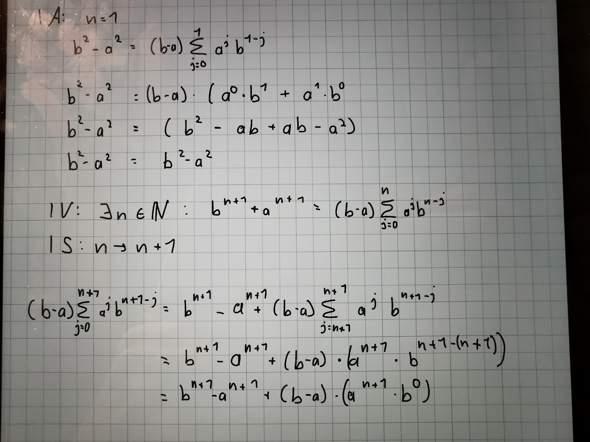
2 Antworten
Du hast tatsächlich nur einen ganz kleinen Fehler gemacht, aber der haut dir das auseinander.
Der erste Schritt ist ja:
Jetzt hast du das auseinandergezogen
Und jetzt hast du den ersten Summanden einfach durch die Induktionannahme ersetzt. Dabei hast du ein winziges +1 übersehen, denn in der Induktionsannahme steht
d. h. der Exponent von b in der Summendarstellung ist hier n-j, bei dir stand aber richtigerweise nach dem Auseinanderziehen n+1-j. Du hast also in jedem Summanden ein b "mehr" in dem Produkt.
Daher ist die richtige Fortsetzung jetzt:
Wenn du das jetzt ausmultiplizierst und b^0=1 einsetzt, bekommst du
Und das wolltest du ja haben.
Es wäre besser, wenn du gerade am Anfang die Schritte einzeln aufschreiben würdest. Dann passiert so etwas nicht so leicht.
Ganz genau, ich habe ein b herausgezogen, darum fällt das +1 da weg. Aber da war dann im letzten Schritt ein Fehler, den habe ich korrigiert. (b^(n+1) statt b^(n+2))
in deiner zweiten Formelzeile muss es auch nicht „n+1+j“ sondern „n+1-j“ heißen... im 2. Exponenten von links... oder?
Deine erste Zeile im Induktionsschritt erklärt sich mir ganz und gar nicht.
Der Term vor dem Gleuchheitszeichen ist ein guter Anfang. Dann müsstest du in der Summe das (n+1) Glied aus der Summe ziehen und sehen, wie du es mit dem (b-a) verarbeiten kannst. Ziel wäre es due Summe so umzugestalten, daß sie dem Summenterm aus der Induktionsanahme entspricht.
Du machst da etwas völlig sinnfreie. Deine Summe beginnt plötzlich nicht mehr bei 0. Warum? Wo sind die anderen Summenglieder hingekommen?
Die sind durch die Induktionsannahme ersetzt worden, allerdings mit einem kleinen Fehler.
Hast du nach "Daher ist die richtige Fortsetzung jetzt:..." jetzt nicht auch das "+1" vergessen?