Extremwertaufgabe quadratische Schachtel?
Hallo, wie ihr im Anhang sehen könnt, brauche ich Hilfe. Es geht wie in der Aufgabe beschrieben, um einen quadratischen Blech mit der Kantenlänge 12 cm. Aus der sollten vier Eckpunkte ausgeschnitten werden. Die weiteren Details im Text, damit es hier nicht zu lang wird.
Wir in der Schule gehen da, wie man sieht, ganz anders vor. Im anderen Blatt seht ihr eine andere Aufgabe, wie wir normalerweise vorgehen würden, doch hier ist es schwieriger für mich. Ich brauche Hilfe bei der Zielfunktion und die Nebenbedingung. Die weiteren Schritte ergeben sich dann von selbst und kann sie berechnen.
Kann mir da jemand bitte weiterhelfen? Ist die Zielfunktion vielleicht V = y^2 • x?


3 Antworten
Guten Abend.
Habe mich soeben auch an einer Lösung versucht und kam auch wie „evtldocha“ auf x=2 mit 128cm^2 :

LG Colin
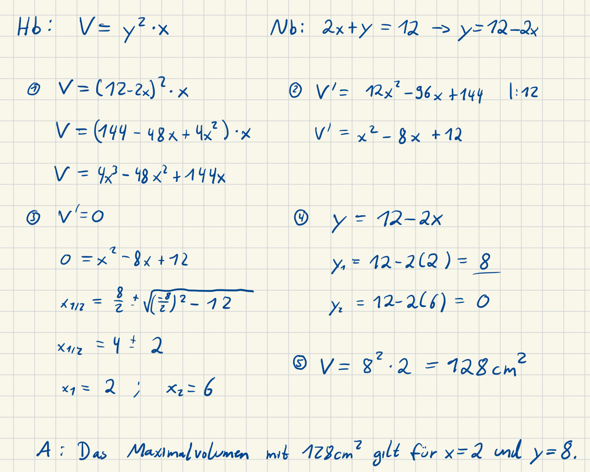
Ich habe das ganze gerade nochmal selbst durchgerechnet zum Check mit der Mitternachtsformel und ohne durch 12 teilen. Ich kam ebenfalls wieder auf 2 und 6. Also weiß ich leider nicht, was bei dir genau beim rechnen schiefgelaufen ist in diesem Schritt. :/
Ich weiß es, hab beim Ausmultiplizieren der zweiten binomischen Formel habe ich ein Vorzeichenfehler gehabt. Jetzt ist es richtig.
In der Schule verwenden wir in diesem Beispiel die Vorzeichentabelle, um zu erkennen, ob es sich um ein absolutes Extremum handelt. Ich müsste dann beide Nullstellen in die Tabelle eintragen und anhand dessen erkennen oder?
V = y^2 • x
... ja, und die Nebenbedingung ist y = 12 - 2x, also ist
und die Ableitung mit der Produkt- und Kettenregel ist dann:
Ich verzichte hier auf das Ausmultiplizieren der Funktion, da sich mit der Produkt- und Kettenregel eine faktorisierte Ableitung ergibt und damit die Nullstellen fast schon abgelesen werden können. Eine der beiden Nullstellen ergibt hier im Hinblick auf die Aufgabe keinen Sinn, da die Lösung die Grundfläche zu null macht (siehe auch den Definitionsbereich 𝔻, für den die Volumenfunktion definiert wurde).
Ab hier sollte es dann einfach weitergehen.
Skizze:

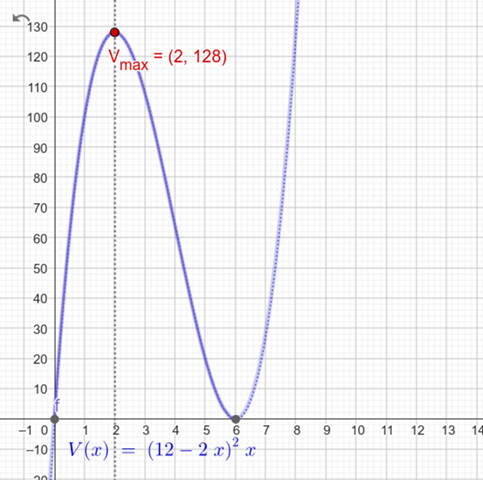
ALs Praxismädel würde ich glaube ich eine Excel Tabelle anlegen.
in Spalte 1 würde ich die Seitenhöhe eintragen, einfach durchnummeriert von 1 bis 59 mm
in Spalte 2 würde ich die daraus resultierende Kantenlänge der Bodenfläche berechnen die Formmel würde dann lauten
=120-2*A1
In der 3. Spalte kannst du dann das Volumen berechnen.
=POTENZ(A2;2)*A1
Man könnte auch einfach Kantenlänge mal Kantenlänge statt Kantenlänge hoch 2 rechnen.
in der 4. Spalte teilst du dann das ergebnis aus der 3. Spalte durch 100
für die richtig guten könnte man auch die formel zusammenfassen
=POTENZ(120-2*A1;2)*A1/100
Wenn du das hast kannst du dann a.) weiter unten mit der folgenden Funktion ermitteln, welcher der größte Wert ist.
=MAX(B1:B59)
Mit der bedingen Formatierung kannst du dann sichtbar machen, wo der höchste Wert ist. oder du legst ein Liniendiagramm an wie dieses

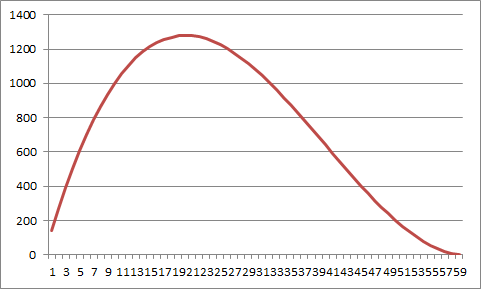
Hallo und vielen Dank für deine Bemühung. Dank euch bin ich bis zur Funktion 3. Grades gekommen. Die 1. Ableitung habe ich auch gemacht, aber eines verstehe ich nicht. Warum sollte man jetzt die Funktion geteilt durch 12 machen? Könnte man das nicht so lassen und es direkt in die Lösungsformel (Mitternachtsformel) einsetzen? Wie ich es gelernt habe, würde es eigentlich am Ergebnis nichts ändern, aber dennoch kommen andere Ergebnisse dann raus, also wenn ich die Funktion nicht durch 12 teile.