Exponentialfunktion Tangente?
Hallo,
ich brauche Hilfe bei der Aufgabe, ich finde nichts wie man sie lösen kann.
wäre sehr dankbar für Vorschläge wie man die Aufgabe 7 lösen kann 😊
lg

2 Antworten
Eine Tangente ist immer eine lineare Funktion, wie du wahrscheinlich weißt. Folgende Funktionsgleichung gilt für lineare Funktionen:
Ich mache es am Beispiel von a!P(0|1), Q(0,5|1)
Nun muss man als erstes m herausbekommen, was man mithilfe der Ableitung macht:Dort setzt man nun den x-Wert des Punktes ein: Für P bekommt man da f'(0) = 2
Nun hat man:Um n herauszubekommen, setzt du einfach den Punkt ein:Und stellst um:Nun hast du die Tangentengleichung für den Punkt P:Bei Q weiß ich jedoch nicht, was verlangt ist, da der Punkt Q nicht auf der Funktion liegt. Ich würde daher davon ausgehen, dass es für Q keine Tangente gibt.
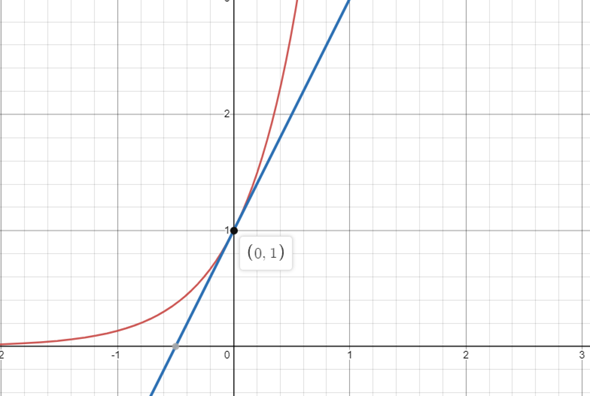
Hier noch einmal eine visuelle Darstellung!
Den Rest solltest du selbst hinbekommen.
Es ist doch f'(0) = 2e^(2*0)
Denn dann kommt im Exponenten 0 heraus und somit wird e^0 = 1 und das dann noch mit der 2, die davor steht, multiplizieren.
Dass du im Netz nichts findest , ist verständlich . Denn du kennst die Stichworte gar nicht ( Tangente im Punkt könnte aber was bringen )
Punkt Steigungsform wäre zielführender
.
.
Denn in deinen Schulsachen müsstest solche Aufgaben finden .
.
.
ich mal b) nehmen
.
f(0) und f(-2) müssen zuerst
4*e^-0.25*0 = 4*1 = 4
4*e^-0.25*-2 = 4*e^0.5 = 4*wurzel(e) = grundet 6.59
.
P(0/4)
Q(-2/6.59)
.
jetzt brauchen die Steigung in P mit der ersten Ableitung
f'(x) = -0.25*4*e^-0.25x =
-e^-0.25x
f'(0) = -e^-0.25*0 = -1
.
Ansatz
ft = -1*x + b
für b brauchen wie P
4 = -1*0 + b
4 = b
Die Tangente heißt
ft(x) = -x + 4
.
danke aber ich habe eine Frage zur Lösung von m.
warum ist das 2 und nicht f(0)= 2e^2*0 ?
danke im Voraus